Pre-process data
dat_shoot_extend <- dat_shoot %>% tidy_shoot_extend()
dat_all <- dat_shoot_extend %>%
filter(doy > 90, doy <= 210) %>%
filter(shoot > 0) %>%
drop_na(barcode) %>%
group_by(species) %>%
mutate(group = str_c(site, year, sep = "_") %>% factor() %>% as.integer()) %>% # site-year level random effects
ungroup() %>%
tidy_treatment_code()
Shoot growth model
Data model
\begin{align*} y_{i,t,s,d} \sim \text{Lognormal}(\mu_{i,t,s,d}, \sigma^2) \end{align*}
Process model
\begin{align*} \mu_{i,t,s,d} &= c+\frac{A_{i,t,s}}{1+e^{-k_{i,t,s}(d-x_{0 i,t,s})}} \newline A_{i,t,s} &= \mu_A + \delta_{A,i}+ \alpha_{A,t,s} \newline x_{0 i,t,s} &= \mu_{x_0} + \delta_{x_0,i}+ \alpha_{x_0,t,s} \newline log(k_{i,t,s}) &= \mu_{log(k)} + \delta_{log(k),i}+ \alpha_{log(k),t,s} \end{align*}
Fixed effects
\begin{align*} \delta_{A,i} &= \beta_{A,1} W_i + \beta_{A,2} D_i + \beta_{A,3} W_i D_i + \beta_{A,4} C_i + \beta_{A,5} W_i C_i \newline \delta_{x_0,i} &= \beta_{x_0,1} W_i + \beta_{x_0,2} D_i + \beta_{x_0,3} W_i D_i + \beta_{x_0,4} C_i + \beta_{x_0,5} W_i C_i \newline \delta_{log(k),i} &= \beta_{log(k),1} W_i + \beta_{log(k),2} D_i + \beta_{log(k),3} W_i D_i + \beta_{log(k),4} C_i + \beta_{log(k),5} W_i C_i \end{align*}
Random effects
\begin{align*} \alpha_{A,t,s} &\sim \text{Normal}(0, \sigma_A^2) \newline \alpha_{x_0,t,s} &\sim \text{Normal}(0, \sigma_{x_0}^2) \newline \alpha_{log(k),t,s} &\sim \text{Normal}(0, \sigma_{log(k)}^2) \end{align*}
Priors
\begin{align*} c &\sim \text{Uniform}(0, 1) \newline \mu_A &\sim \text{Uniform}(1, 6) \newline \beta_A &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 1 & 0 & 0 & 0 & 0 \newline 0 & 1 & 0 & 0 & 0 \newline 0 & 0 & 1 & 0 & 0 \newline 0 & 0 & 0 & 1 & 0 \newline 0 & 0 & 0 & 0 & 1 \newline \end{pmatrix} )\newline \sigma_A^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \newline \mu_{x_0} &\sim \text{Uniform}(120, 180) \newline \beta_{x_0} &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 100 & 0 & 0 & 0 & 0 \newline 0 & 100 & 0 & 0 & 0 \newline 0 & 0 & 100 & 0 & 0 \newline 0 & 0 & 0 & 100 & 0 \newline 0 & 0 & 0 & 0 & 100 \newline \end{pmatrix} )\newline \sigma_{x_0}^2 &\sim \text{Truncated Normal}(0, 100, 0, \infty) \newline \mu_{log(k)} &\sim \text{Uniform}(-4, -1) \newline \beta_{log(k)} &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 0.04 & 0 & 0 & 0 & 0 \newline 0 & 0.04 & 0 & 0 & 0 \newline 0 & 0 & 0.04 & 0 & 0 \newline 0 & 0 & 0 & 0.04 & 0 \newline 0 & 0 & 0 & 0 & 0.04 \newline \end{pmatrix} )\newline \sigma_{log(k)}^2 &\sim \text{Truncated Normal}(0, 0.04, 0, \infty) \newline \sigma^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \end{align*}
calc_bayes_all(
data = dat_all,
independent_priors = F, # do not use species-specific empirical informative priors
uniform_priors = T, # use uniform priors
intui_param = F, # regular parameterization with asym, xmid, logk
num_iterations = 50000,
nthin = 5,
path = "alldata/intermediate/shootmodeling/uni/",
num_cores = 20
)
calc_bayes_derived(path = "alldata/intermediate/shootmodeling/uni/", num_cores = 20)
plot_bayes_all(path = "alldata/intermediate/shootmodeling/uni/", num_cores = 20)
MCMC
df_bayes_all <- read_bayes_all(path = "alldata/intermediate/shootmodeling/uni/", full_factorial = T, derived = F, tidy_mcmc = F)
p_bayes_diagnostics <- plot_bayes_diagnostics(df_MCMC = df_bayes_all %>% filter(species == "queru"), plot_corr = F)
p_bayes_diagnostics$p_MCMC
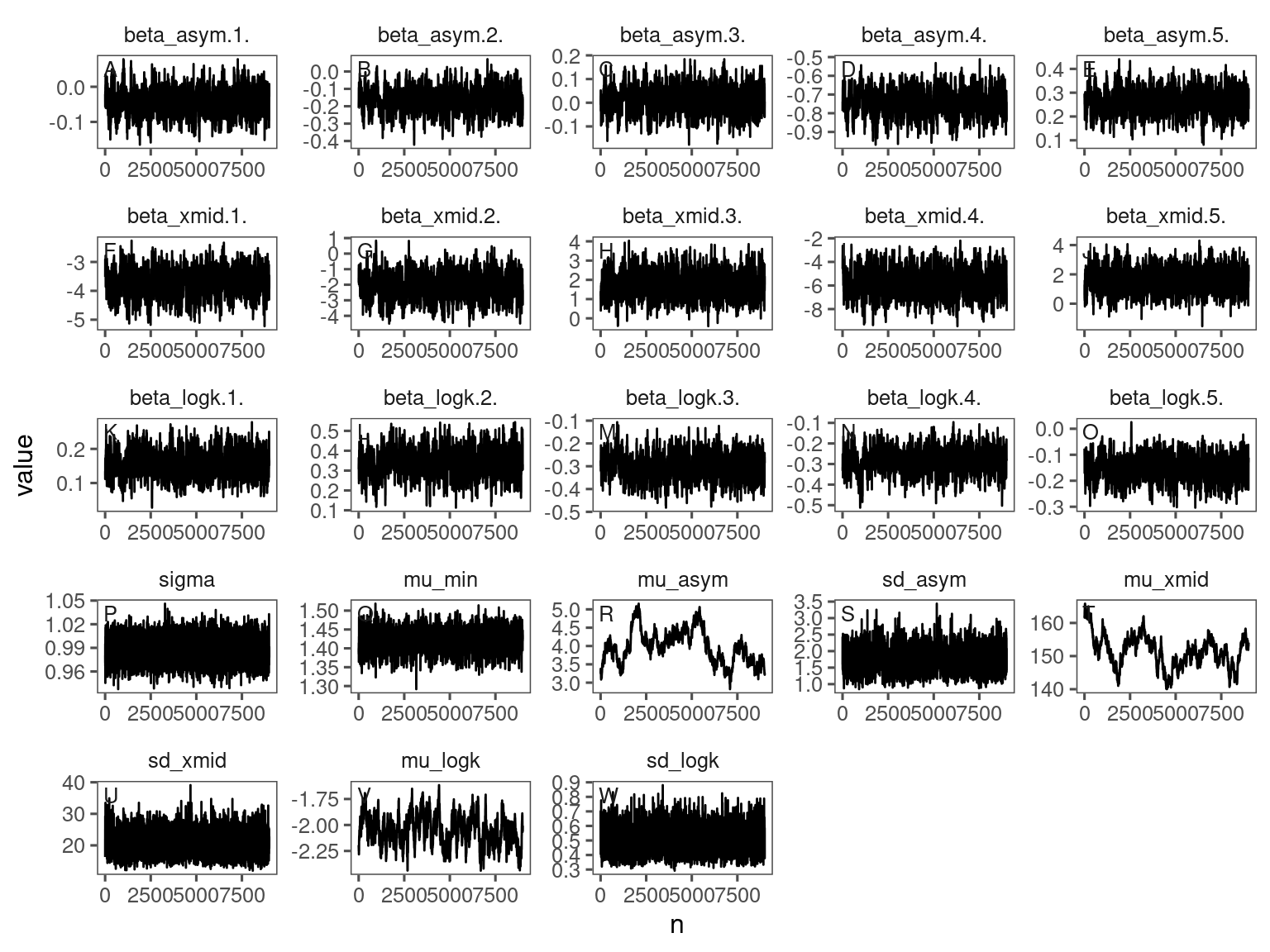
p_bayes_diagnostics$p_posterior
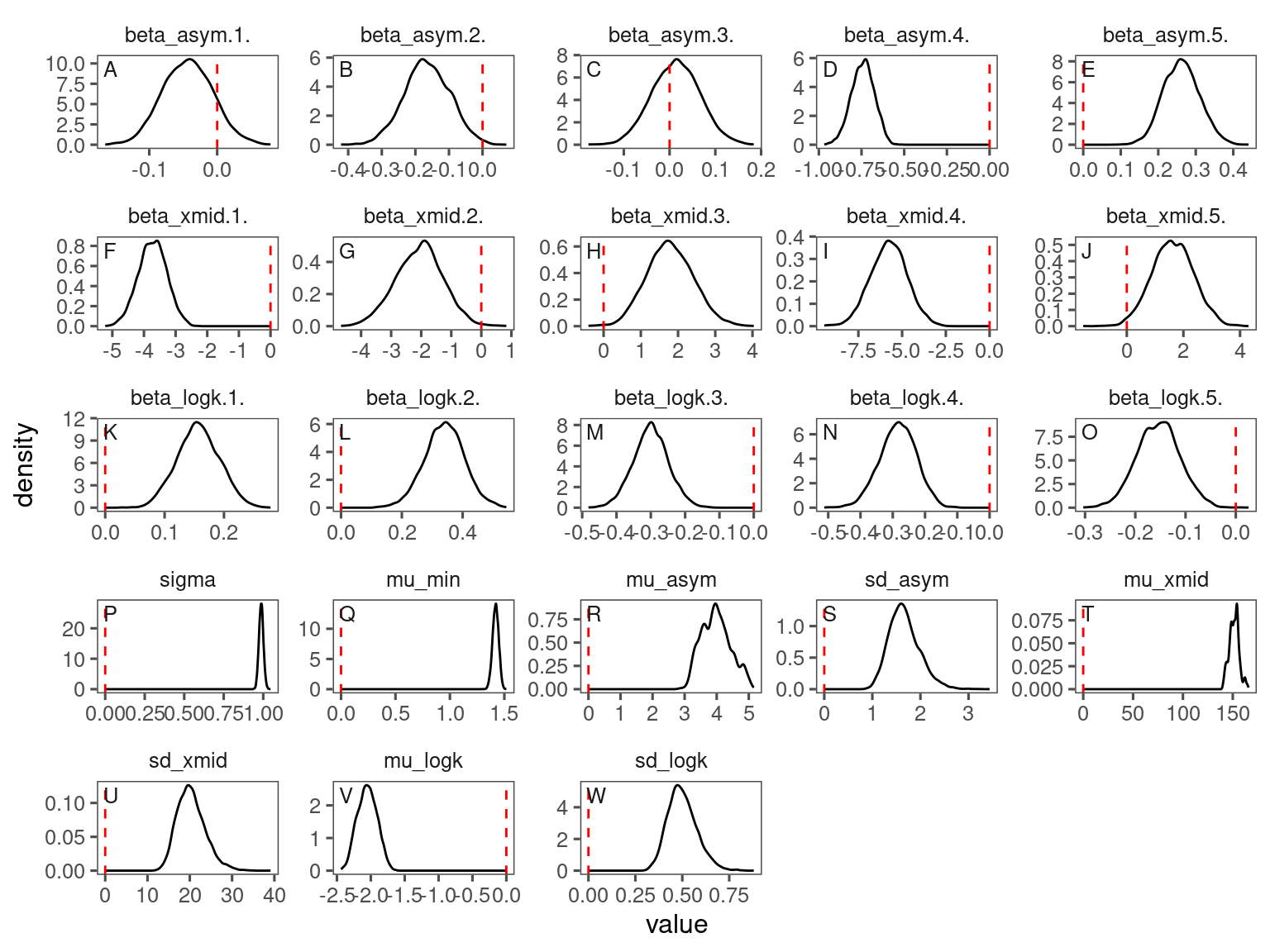
Conditional predictions
df_bayes_pred_all <- read_bayes_all(path = "alldata/intermediate/shootmodeling/uni/", full_factorial = T, content = "predict")
p_bayes_predict <- plot_bayes_predict(
data = dat_all %>% filter(species == "queru"),
data_predict = df_bayes_pred_all %>% filter(species == "queru"),
vis_log = T,
vis_ci = F
)
p_bayes_predict$p_overlay
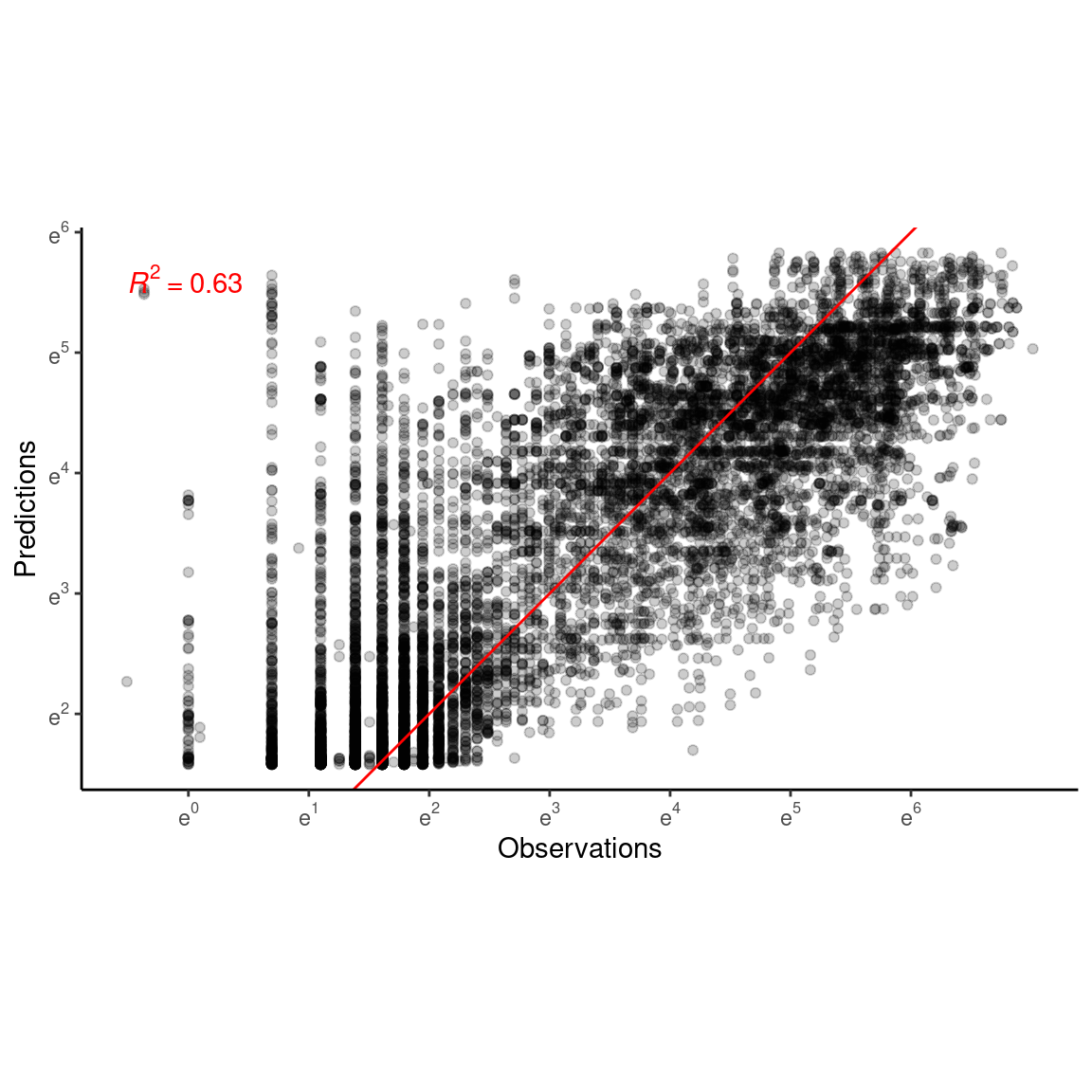
Accuracy
p_bayes_predict$p_accuracy
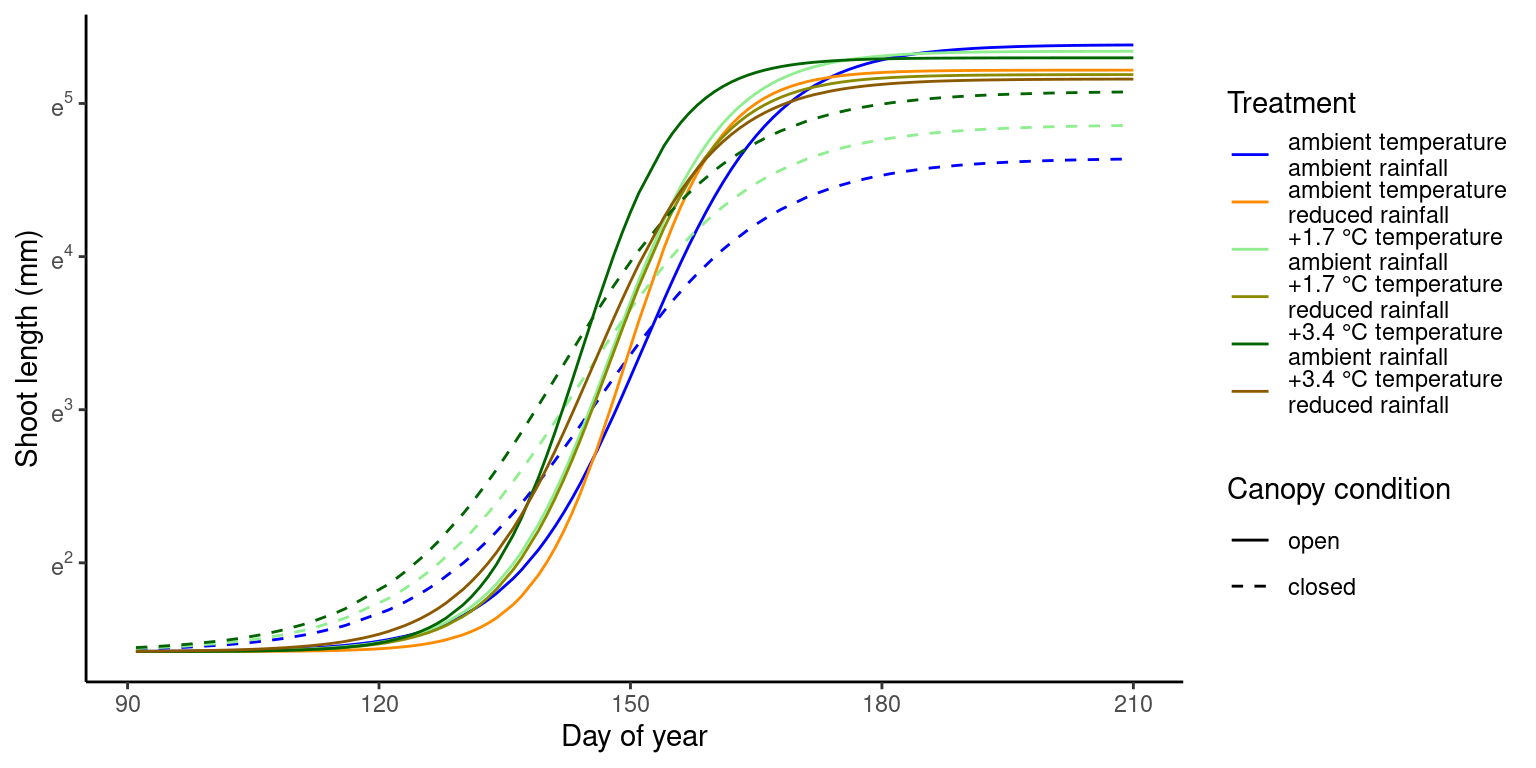
Marginal predictions
df_bayes_pred_marginal_all <- read_bayes_all(path = "alldata/intermediate/shootmodeling/uni/", full_factorial = T, content = "predict_marginal")
p_bayes_predict <- plot_bayes_predict(
data_predict = df_bayes_pred_marginal_all %>% filter(species == "queru"),
vis_log = T,
vis_ci = F
)
p_bayes_predict$p_predict
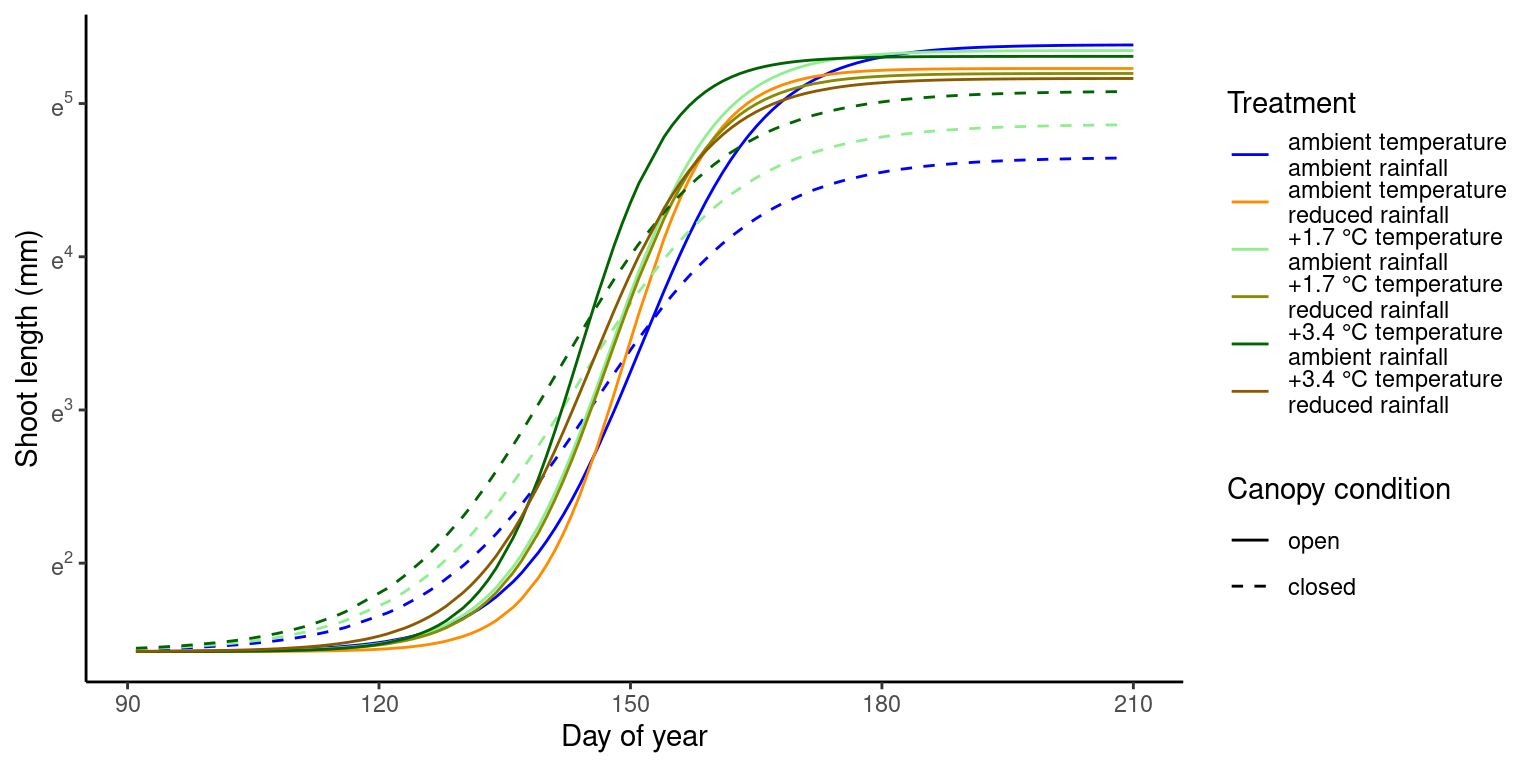
Read in summary of inferred parameters
df_bayes_all <- read_bayes_all(path = "alldata/intermediate/shootmodeling/uni/", full_factorial = T, derived = T, tidy_mcmc = T) %>%
tidy_species_name()
Intercept
p_bayes_summ <- plot_bayes_summary(df_bayes_all, option = "mu", derived_metric = "no")
p1 <- p_bayes_summ$p_coef_line
p_bayes_summ <- plot_bayes_summary(df_bayes_all, option = "mu", derived_metric = "only")
p2 <- p_bayes_summ$p_coef_line
p1 / (p2 + tagger::tag_facets(
tag_suffix = "",
tag_pool = c("D", "E", "F", "G")
))
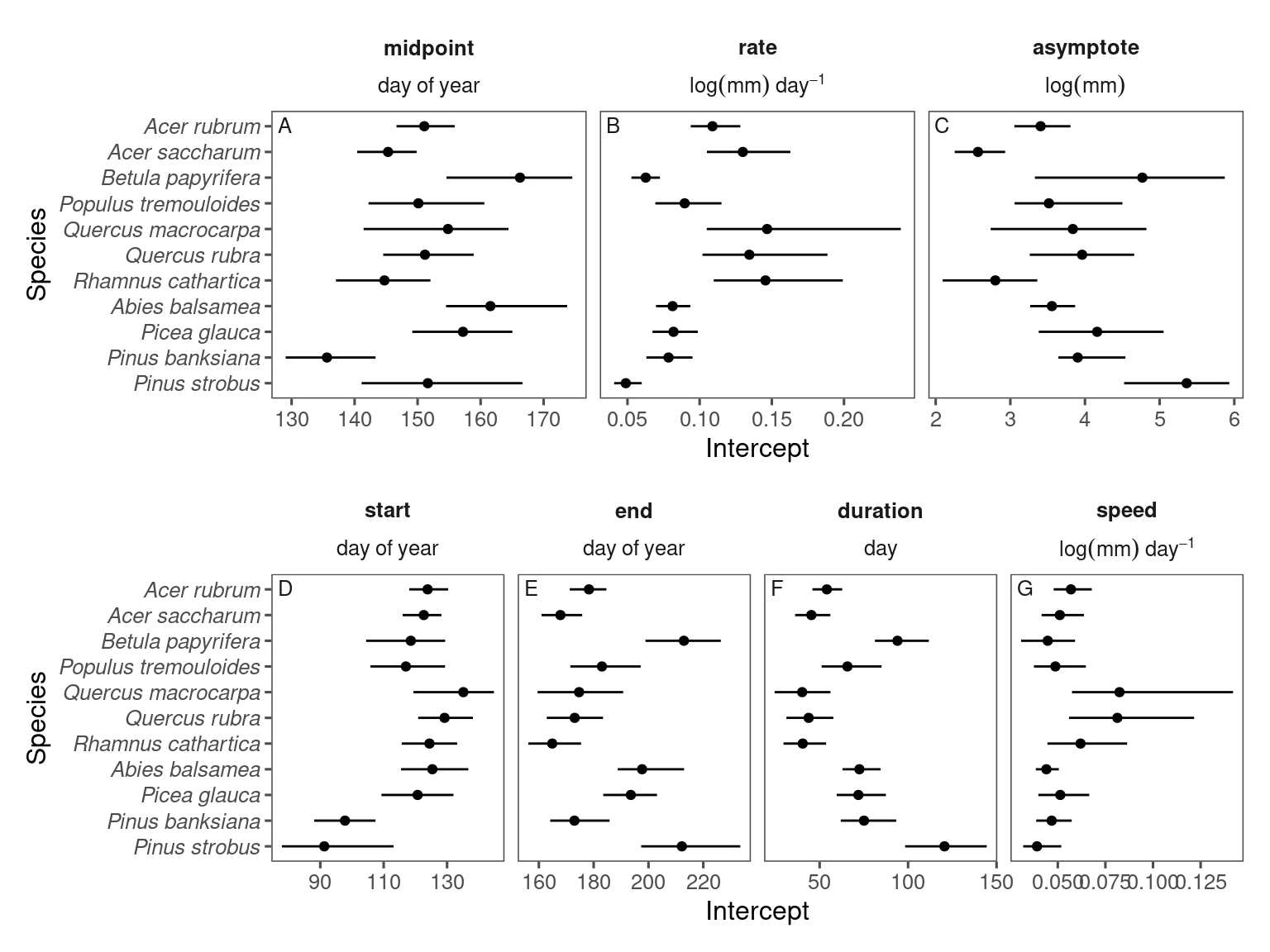
Coefficients
p_bayes_summ <- plot_bayes_summary(df_bayes_all, option = "coef", derived_metric = "no")
p_bayes_summ$p_coef_line
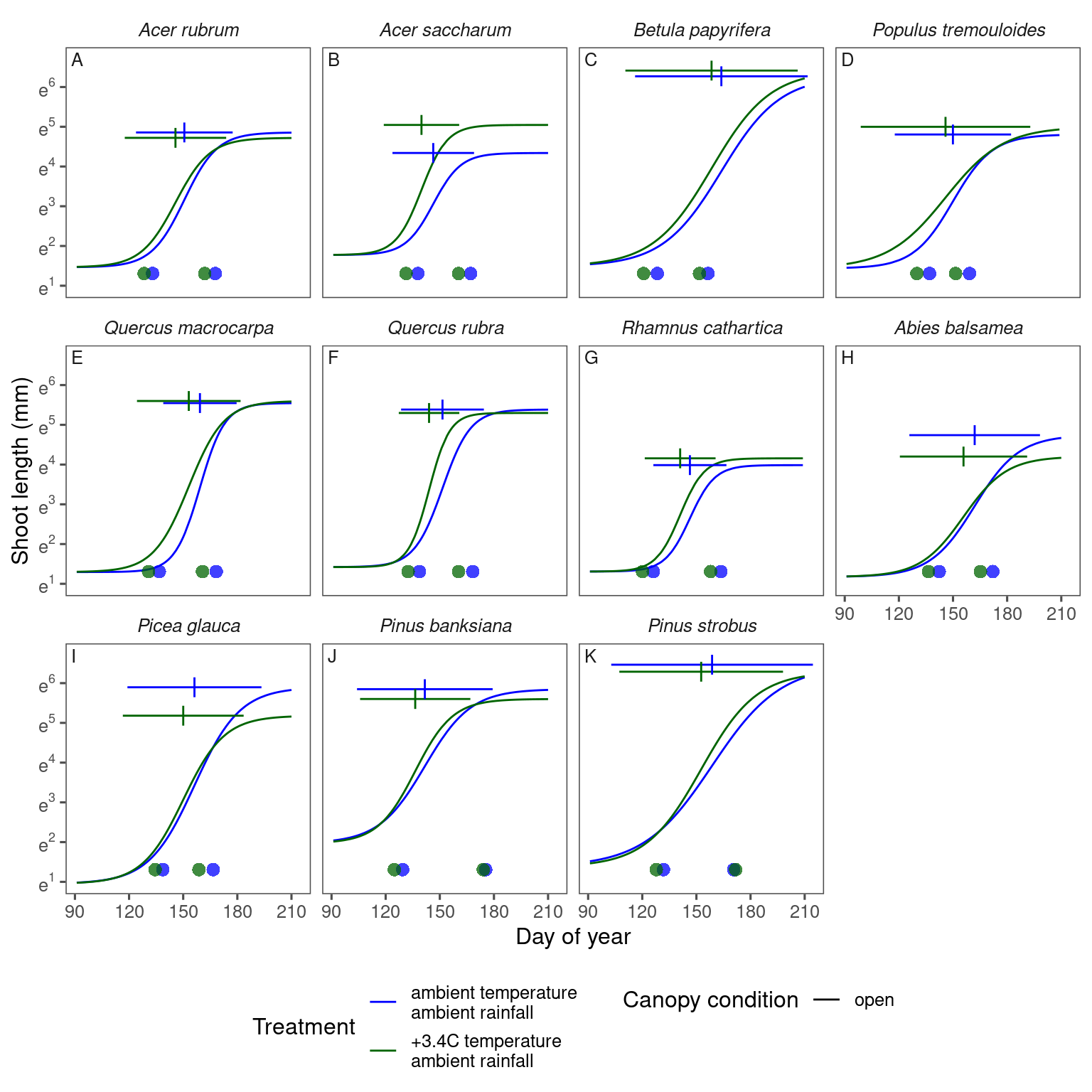
p_bayes_summ <- plot_bayes_summary(df_bayes_all, option = "coef", derived_metric = "only")
p_bayes_summ$p_coef_line
Synthesis
Ordination of intercept
df_shoot_mu <- read_bayes_all(path = "alldata/intermediate/shootmodeling/uni/", full_factorial = T, derived = T, tidy_mcmc = T, content = "mcmc") %>%
summ_mcmc(option = "mu", stats = "median") %>%
tidy_species_name()
plot_ordination(df_shoot_mu, v_treatment = NULL)
df_shoot_coef <- read_bayes_all(path = "alldata/intermediate/shootmodeling/uni/", full_factorial = T, derived = T, tidy_mcmc = T, content = "mcmc") %>%
summ_mcmc(option = "all", stats = "median") %>%
tidy_species_name()
df_shoot_pred <- read_bayes_all(path = "alldata/intermediate/shootmodeling/uni/", full_factorial = T, derived = F, content = "predict_marginal") %>%
tidy_species_name()
# df_phenophase_spring_coef <- read_bayes_all(path = "alldata/intermediate/phenophase/uni/", season = "spring", full_factorial = T, derived = T, tidy_mcmc = T, content = "mcmc") %>%
# summ_mcmc(option = "all", stats = "median") %>%
# tidy_species_name() %>%
# tidy_phenophase_name(season = "spring")
Marginal predictions
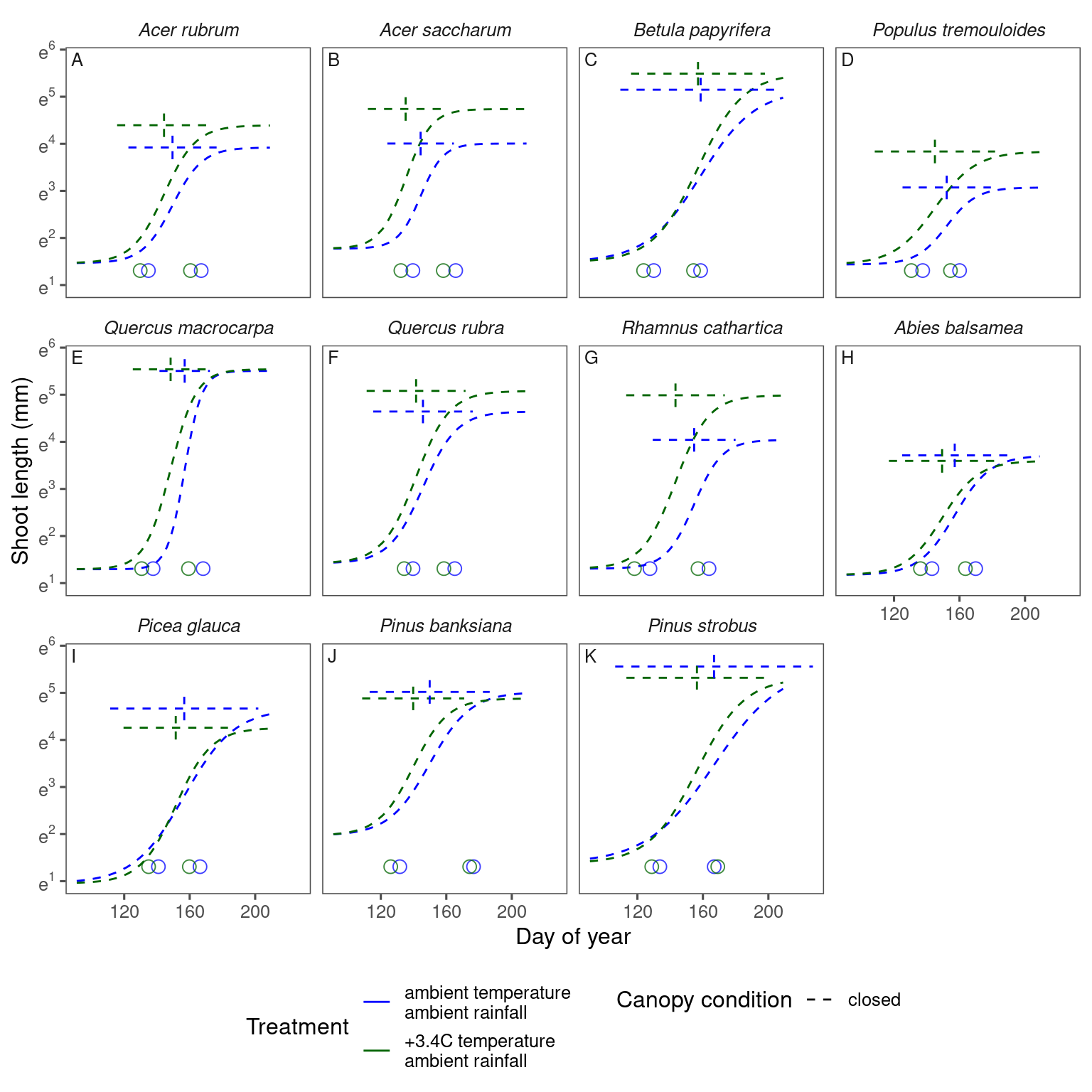
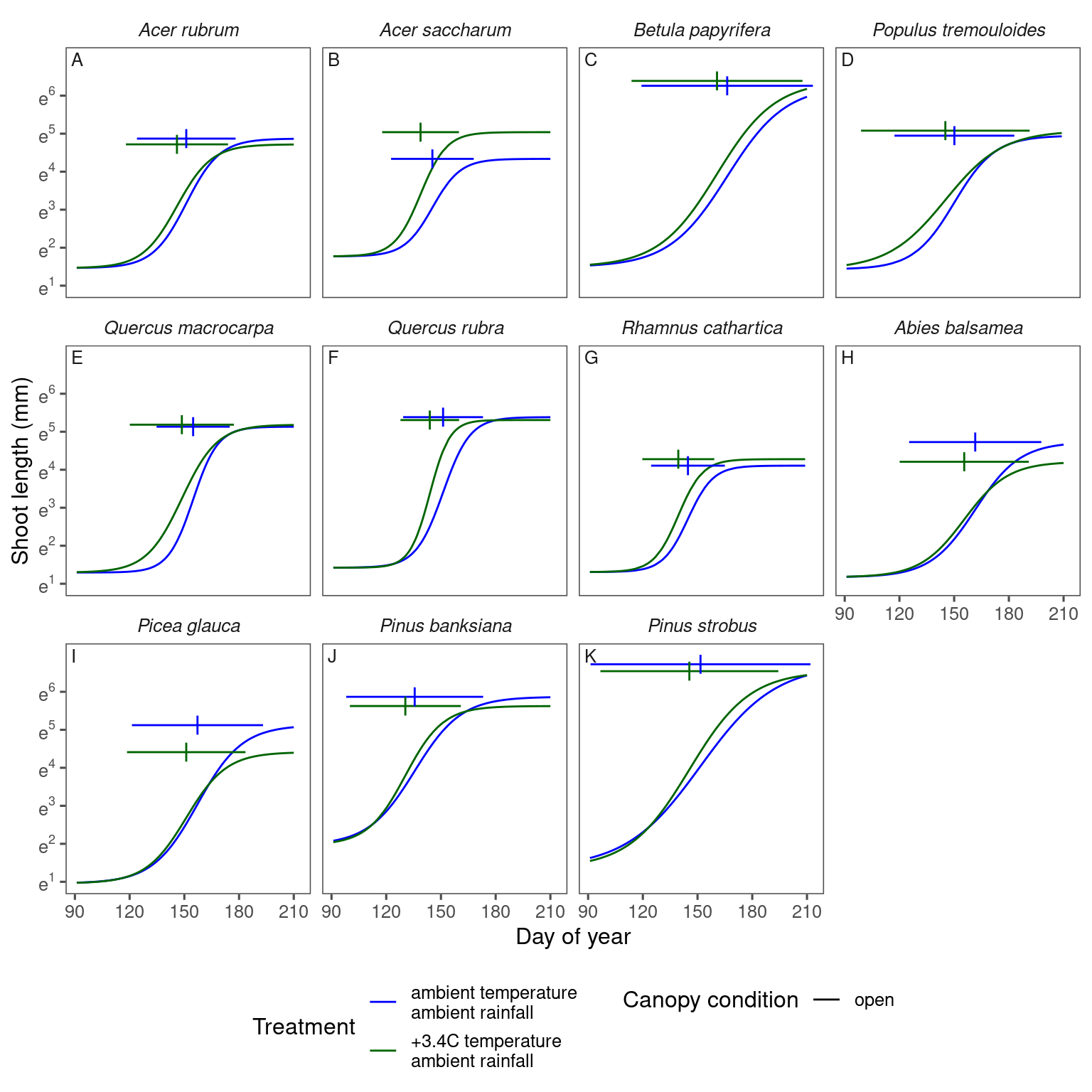
plot_synthesis(df_shoot_pred, df_shoot_coef, treatment = "warming")
plot_synthesis(df_shoot_pred, df_shoot_coef, treatment = "warming | closed")
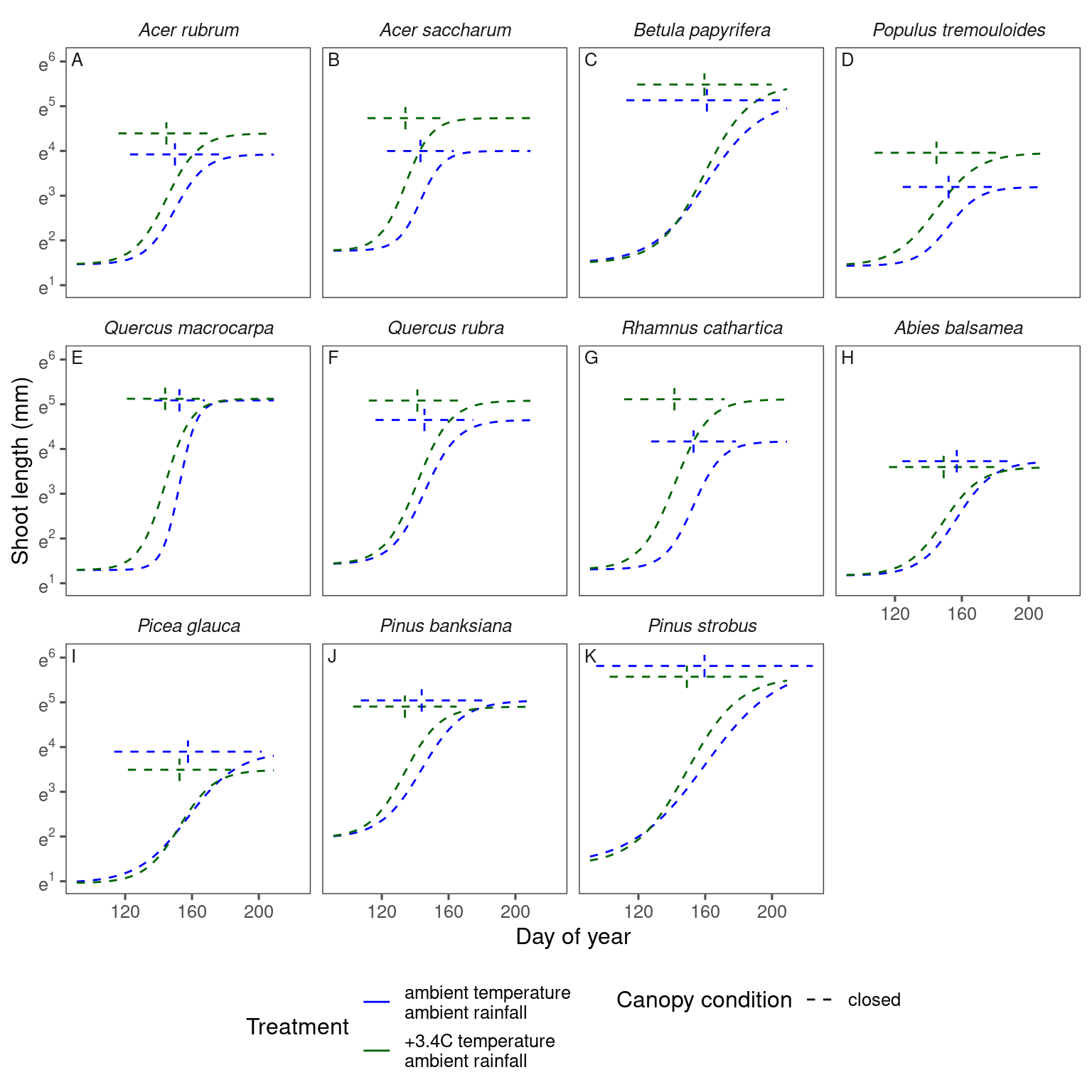
plot_synthesis(df_shoot_pred, df_shoot_coef, treatment = "closed")
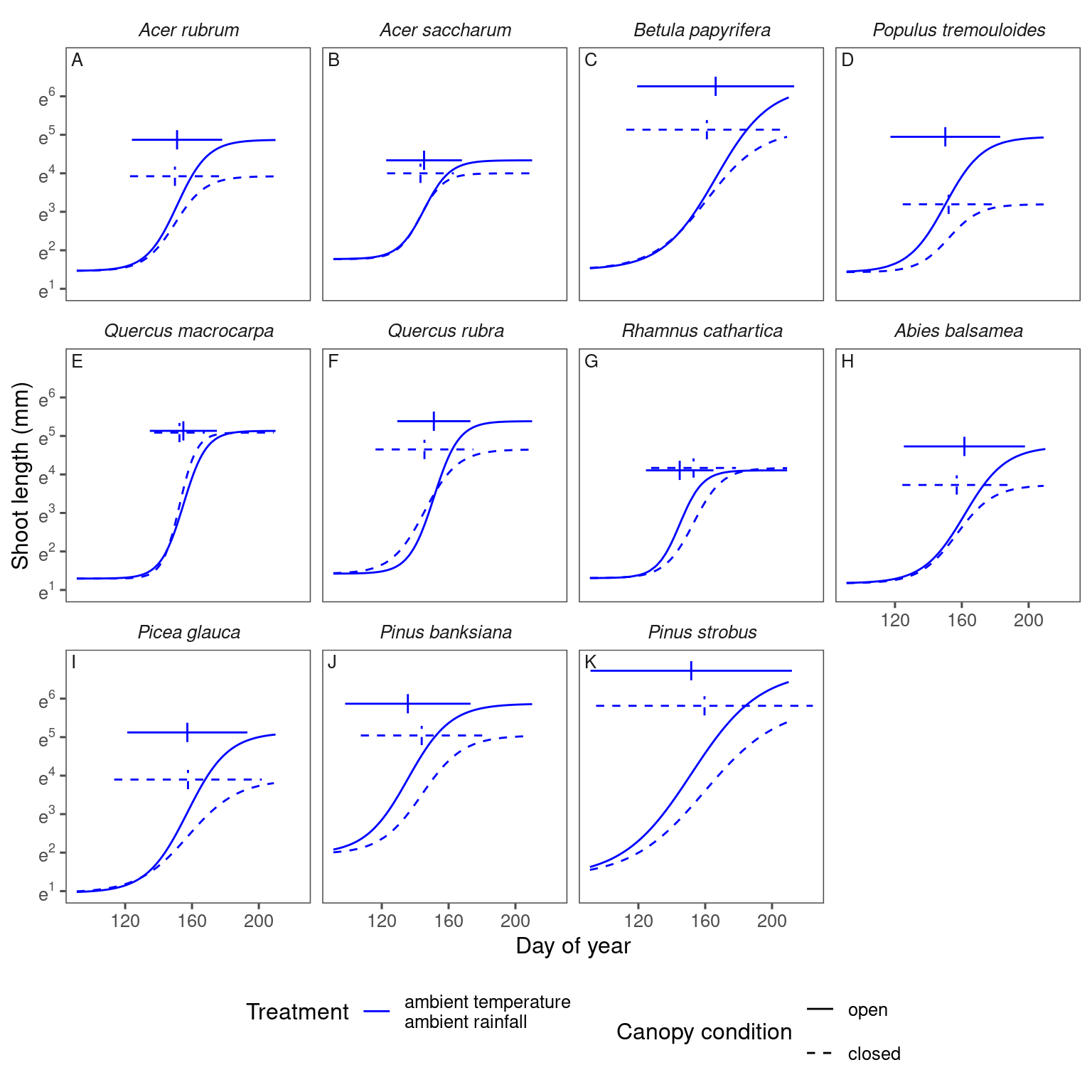
plot_synthesis(df_shoot_pred, df_shoot_coef, treatment = "drying")
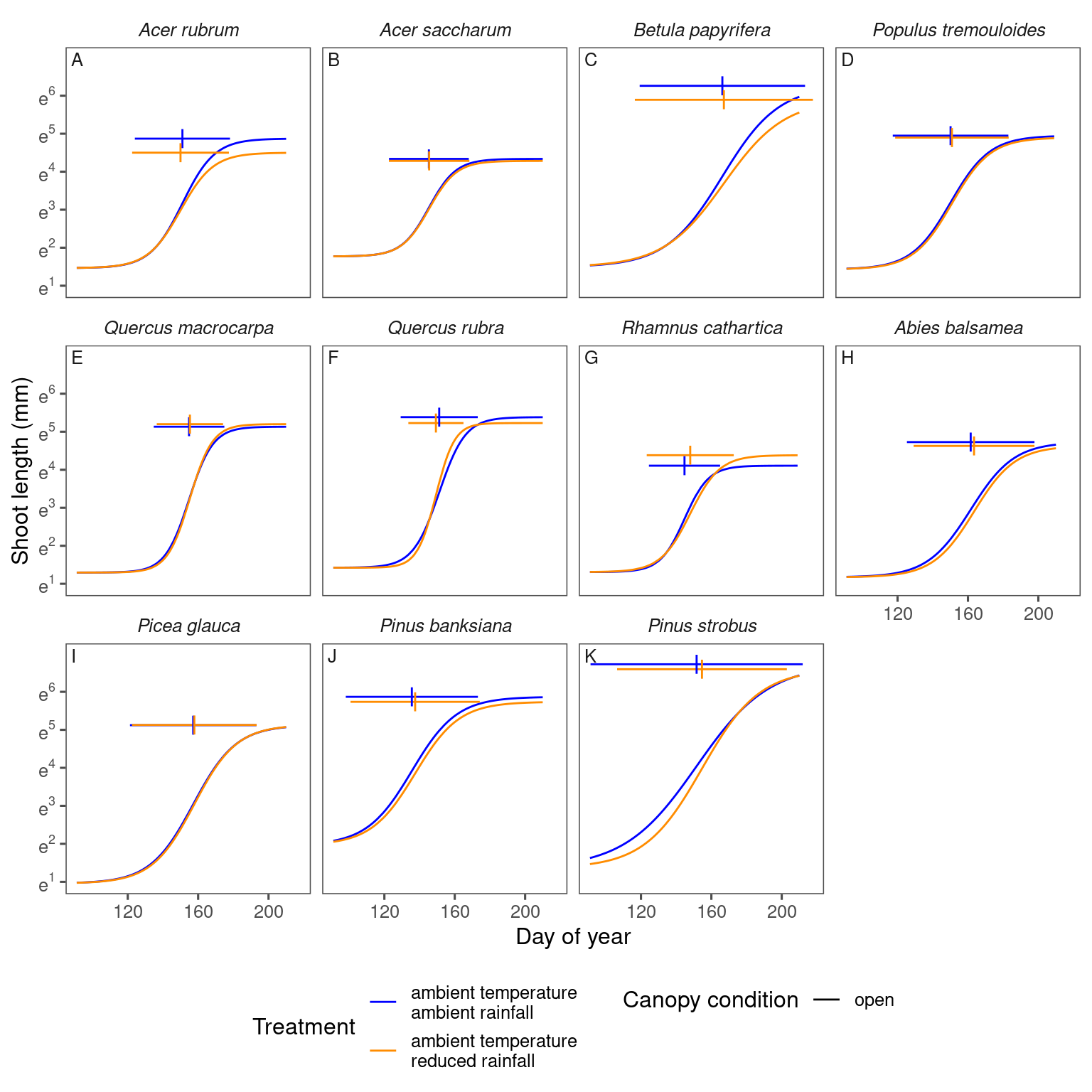
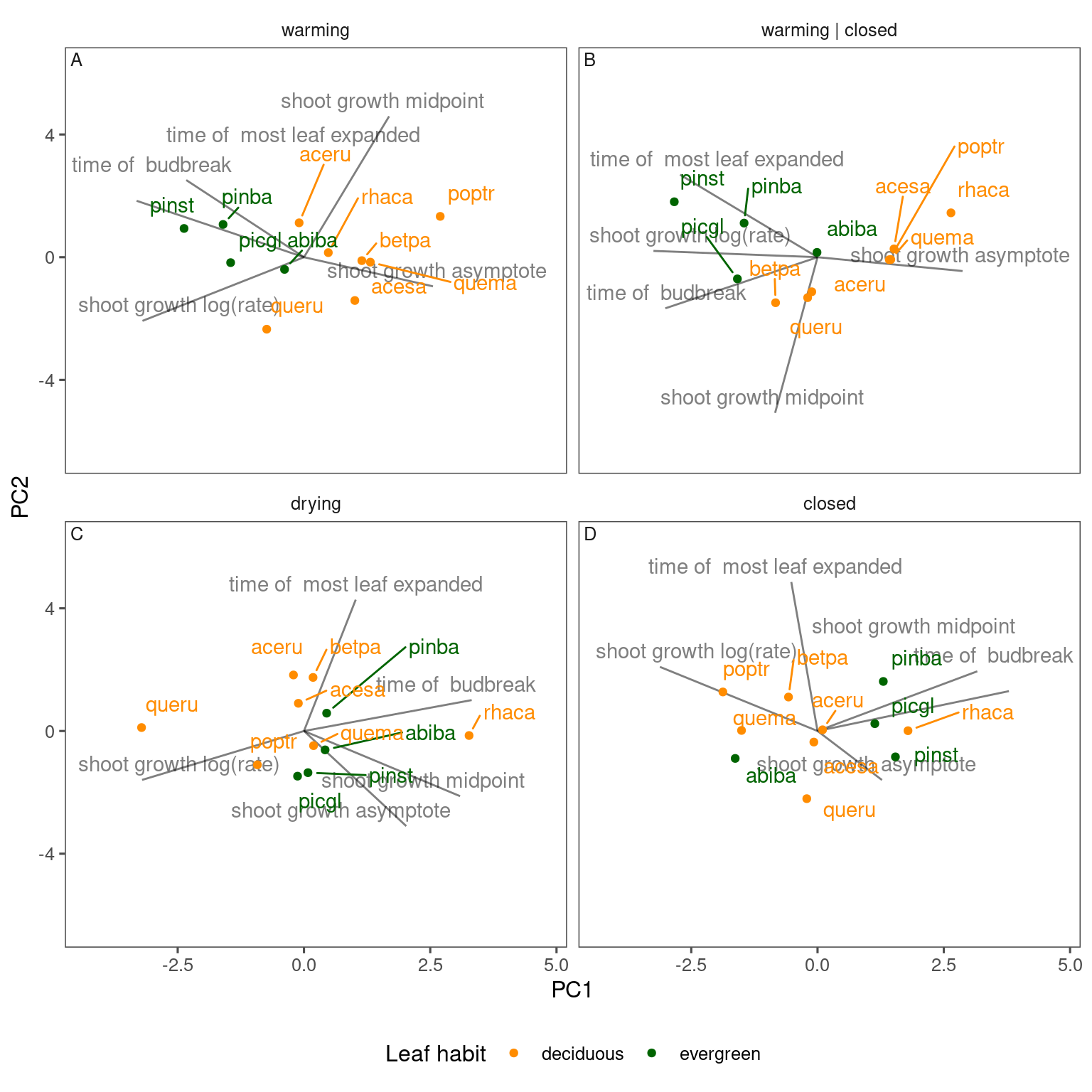
Ordination of responses
plot_ordination(df_shoot_coef, v_treatment = c("warming", "warming | closed", "closed", "drying"))
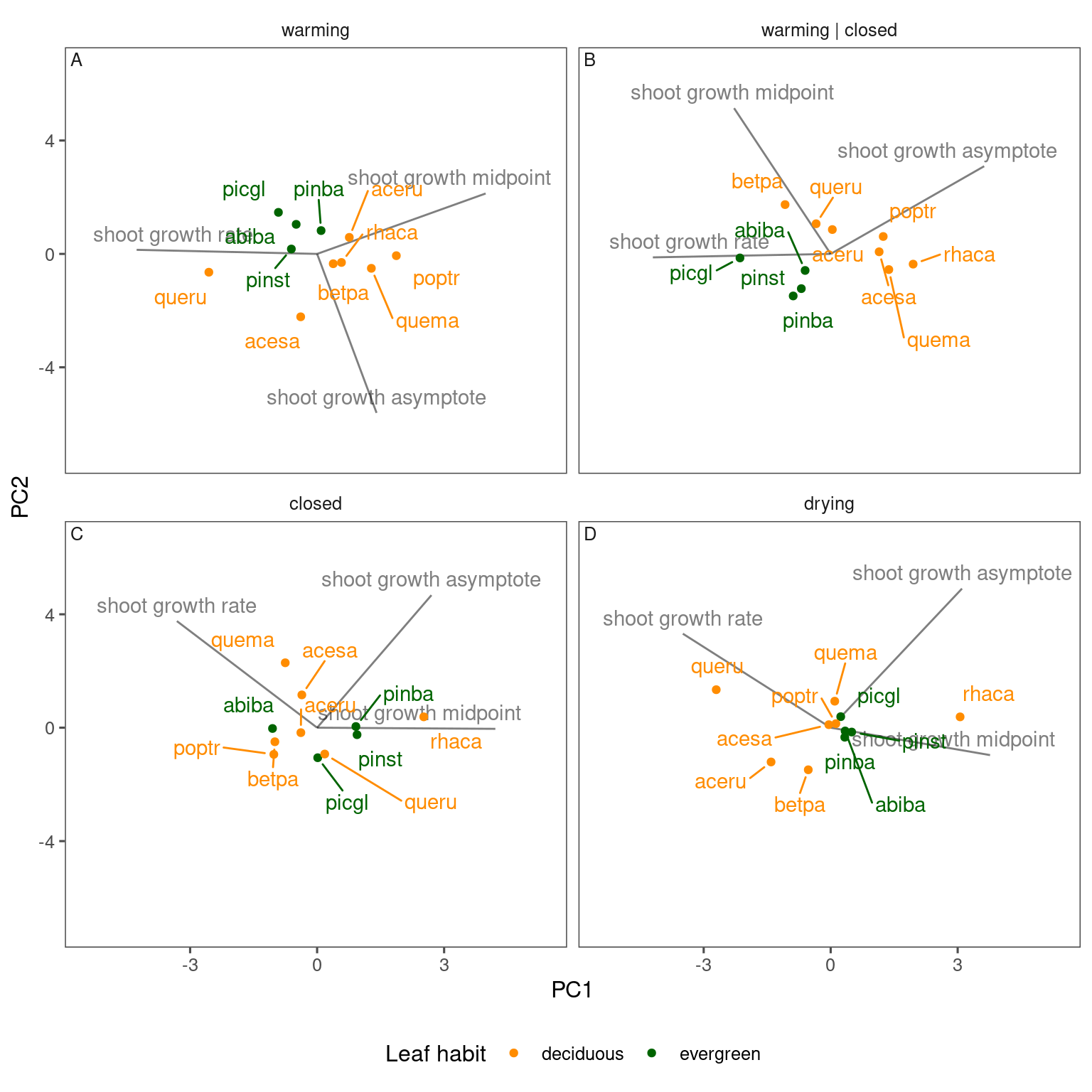
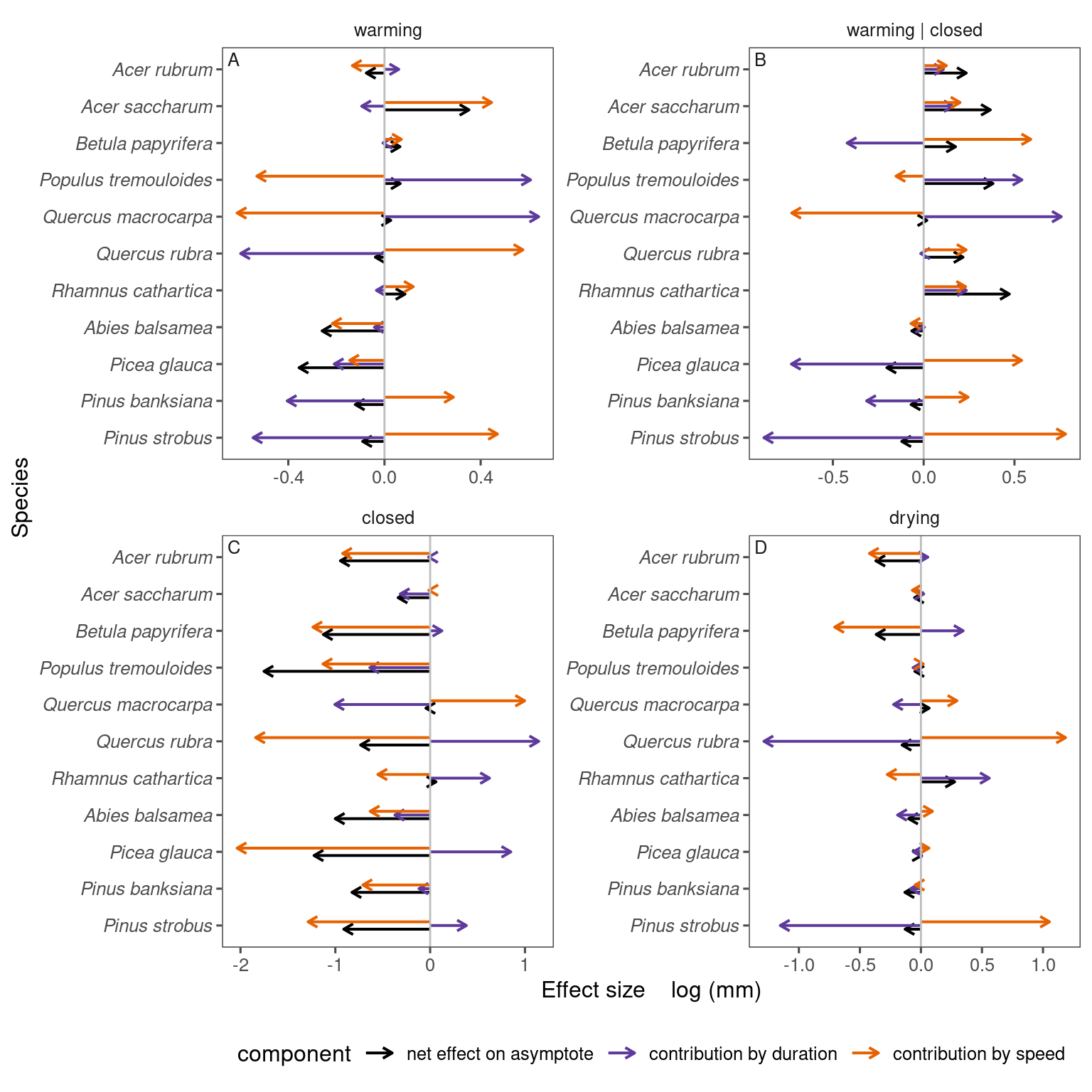
Partitioning contributions of duration and speed to asymptote changes
df_partition <- calc_partition(df_shoot_coef)
plot_partition(df_partition, v_treatment = c("warming", "warming | closed", "closed", "drying"))