Bayesian model 5

Shoot-level random effects. Ignore year-level differences. Treatments as covariates.

Model

Data model

\begin{align*} y_{i,d} \sim \text{Lognormal}(\mu_{i,d}, \sigma^2) \end{align*}

Process model

\begin{align*} \mu_{i,d} &= c+\frac{A_{i}}{1+e^{-k_{i}(d-x_{0 i})}} \newline A_{i} &= \mu_A + \delta_{A,i}+ \alpha_{A,i} \newline x_{0 i} &= \mu_{x_0} + \delta_{x_0,i}+ \alpha_{x_0,i} \newline
log(k_{i}) &= \mu_{log(k)} + \delta_{log(k),i}+ \alpha_{log(k),i} \end{align*}

Fixed effects

\begin{align*} \delta_{A,i} &= \beta_{A,1} T_i + \beta_{A,2} D_i + \beta_{A,3} T_i D_i \newline \delta_{x_0,i} &= \beta_{x_0,1} T_i + \beta_{x_0,2} D_i + \beta_{x_0,3} T_i D_i \newline \delta_{log(k),i} &= \beta_{log(k),1} T_i + \beta_{log(k),2} D_i + \beta_{log(k),3} T_i D_i \end{align*}

Random effects

\begin{align*} \alpha_{A,i} &\sim \text{Normal}(0, \sigma_A^2) \newline \alpha_{x_0,i} &\sim \text{Normal}(0, \sigma_{x_0}^2) \newline \alpha_{log(k),i} &\sim \text{Normal}(0, \sigma_{log(k)}^2) \end{align*}

Priors

\begin{align*} c &\sim \text{Normal}(0, 1) \newline \mu_A &\sim \text{Normal}(5, 1) \newline \beta_A &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 1 & 0 & 0 \newline 0 & 1 & 0 \newline 0 & 0 & 1 \newline \end{pmatrix} )\newline \sigma_A^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \newline \mu_{x_0} &\sim \text{Normal}(160, 100) \newline \beta_{x_0} &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 100 & 0 & 0 \newline 0 & 100 & 0 \newline 0 & 0 & 100 \newline \end{pmatrix} )\newline \sigma_{x_0}^2 &\sim \text{Truncated Normal}(0, 100, 0, \infty) \newline \mu_{log(k)} &\sim \text{Normal}(-2, 0.04) \newline \beta_{log(k)} &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 0.04 & 0 & 0 \newline 0 & 0.04 & 0 \newline 0 & 0 & 0.04 \newline \end{pmatrix} )\newline \sigma_{log(k)}^2 &\sim \text{Truncated Normal}(0, 0.04, 0, \infty) \newline \sigma^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \end{align*}

Prepare data

dat_5 <- dat_shoot_cov %>%
  filter(species == "queru", canopy == "open", site == "cfc") %>%
  filter(shoot > 0) %>%
  drop_na(barcode) %>%
  mutate(slot = if_else(is.na(slot), "", slot)) %>%
  mutate(group = str_c(barcode, slot, sep = "_") %>% factor() %>% as.integer()) %>%
  mutate(heat_trt = factor(heat_name, levels = c("ambient", "+1.7C", "+3.4C"), labels = c(0, 1, 2)) %>% as.character() %>% as.integer()) %>%
  mutate(water_trt = factor(water_name, levels = c("ambient", "reduced"), labels = c(0, 1)) %>% as.character() %>% as.integer())

Fit model

df_MCMC_5 <- calc_bayes_fit(
  data = dat_5 %>% mutate(tag = "training"),
  version = 5
)
write_rds(df_MCMC_5, "alldata/intermediate/shootmodeling/df_MCMC_5.rds")

df_MCMC_5 <- read_rds("alldata/intermediate/shootmodeling/df_MCMC_5.rds") %>% tidy_mcmc(dat_5)
p_bayes_diagnostics <- plot_bayes_diagnostics(df_MCMC = df_MCMC_5, plot_corr = F)
p_bayes_diagnostics$p_MCMC

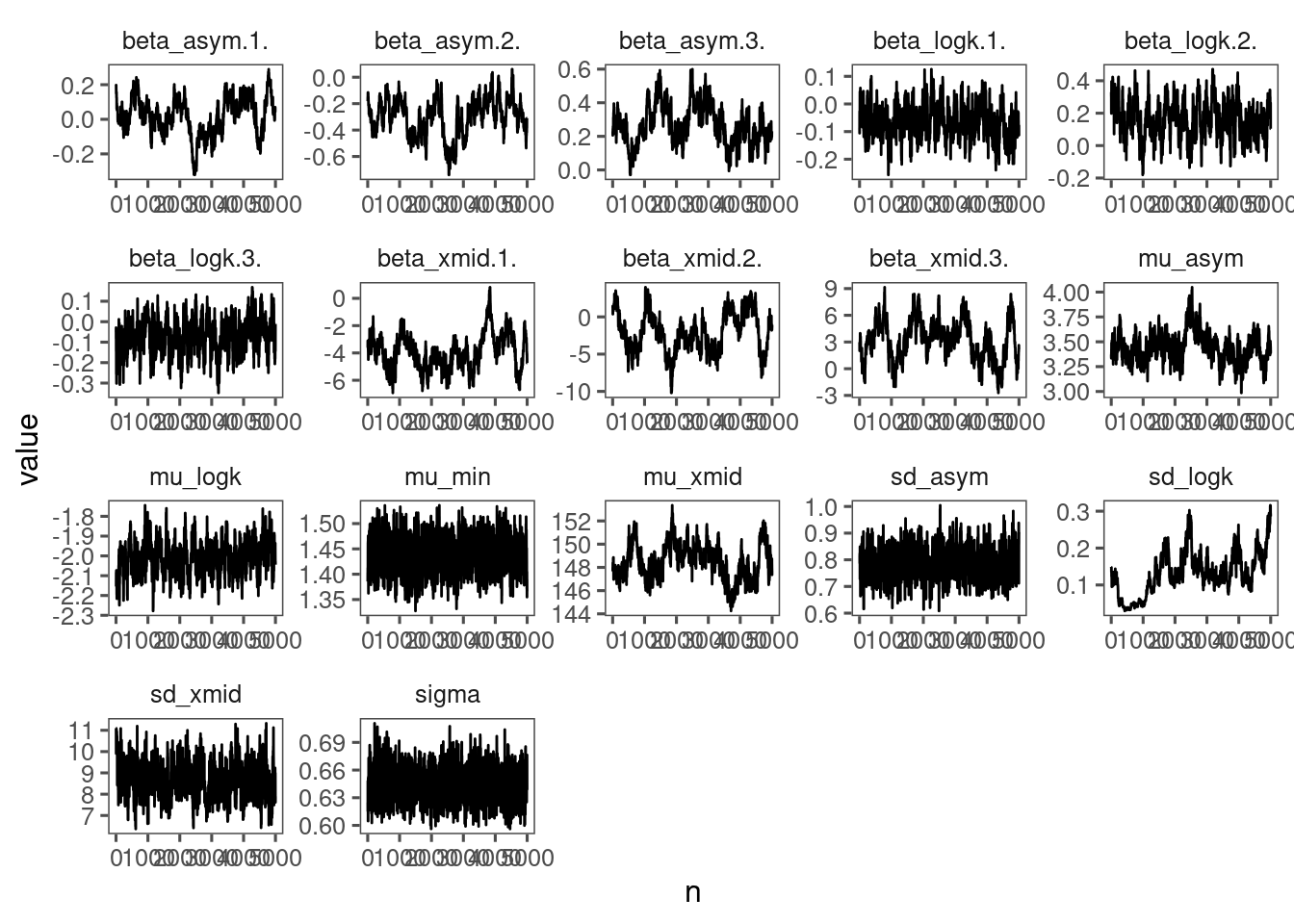
p_bayes_diagnostics$p_posterior

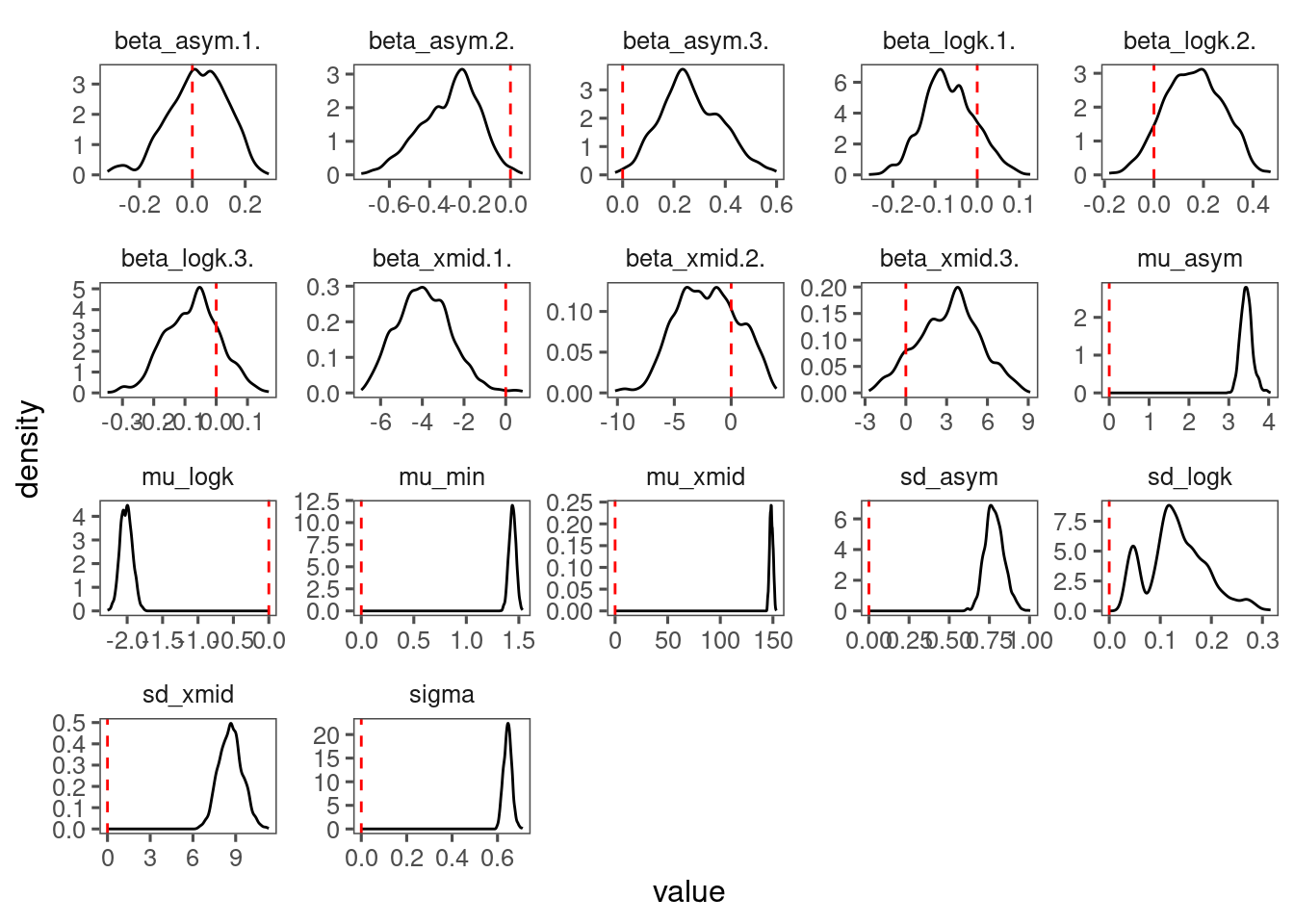
p_bayes_diagnostics$p_coefficient

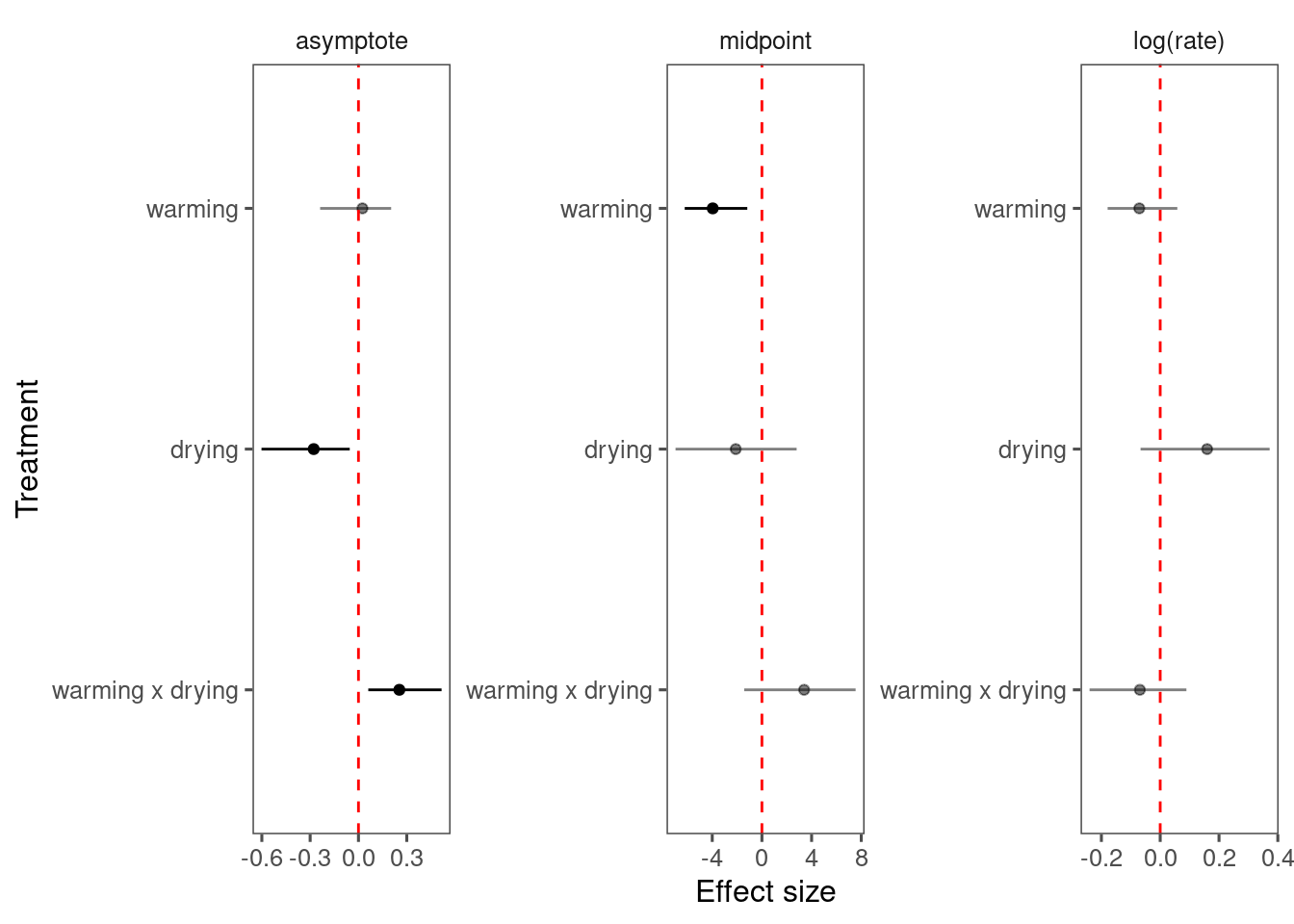
Mixing only slightly better than model 4 but still too many individuals. Might need longer MCMC chains.

Make predictions

df_pred_5 <- calc_bayes_predict(
  data = dat_5 %>%
    distinct(group, heat_trt, water_trt, doy),
  df_MCMC = df_MCMC_5,
  version = 5
)
write_rds(df_pred_5, "alldata/intermediate/shootmodeling/df_pred_5.rds")

df_pred_5 <- read_rds("alldata/intermediate/shootmodeling/df_pred_5.rds")
p_bayes_predict <- plot_bayes_predict(
  data = dat_5,
  data_predict = df_pred_5,
  vis_log = T
)

p_bayes_predict$p_original

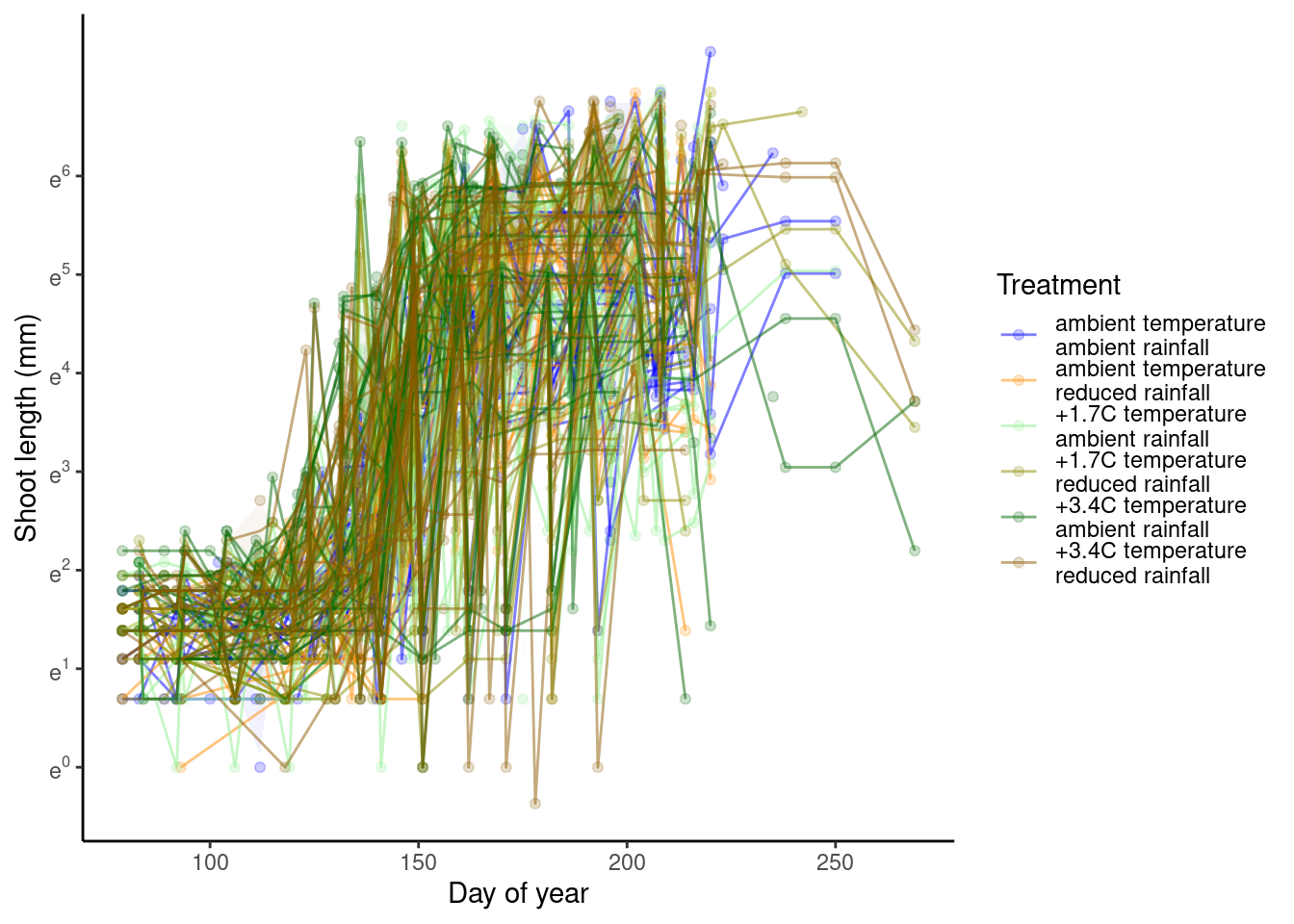
p_bayes_predict$p_overlay

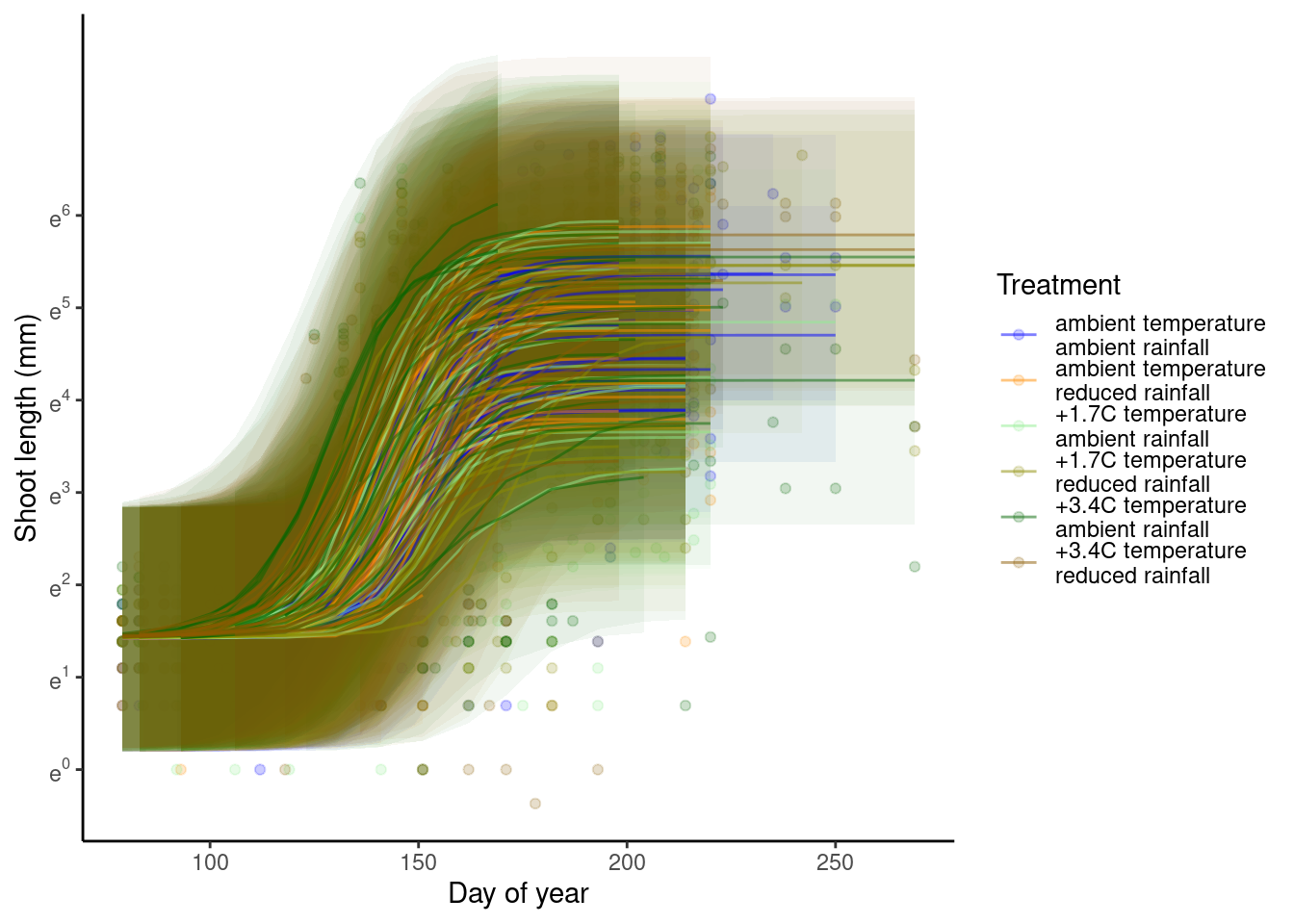
p_bayes_predict$p_accuracy

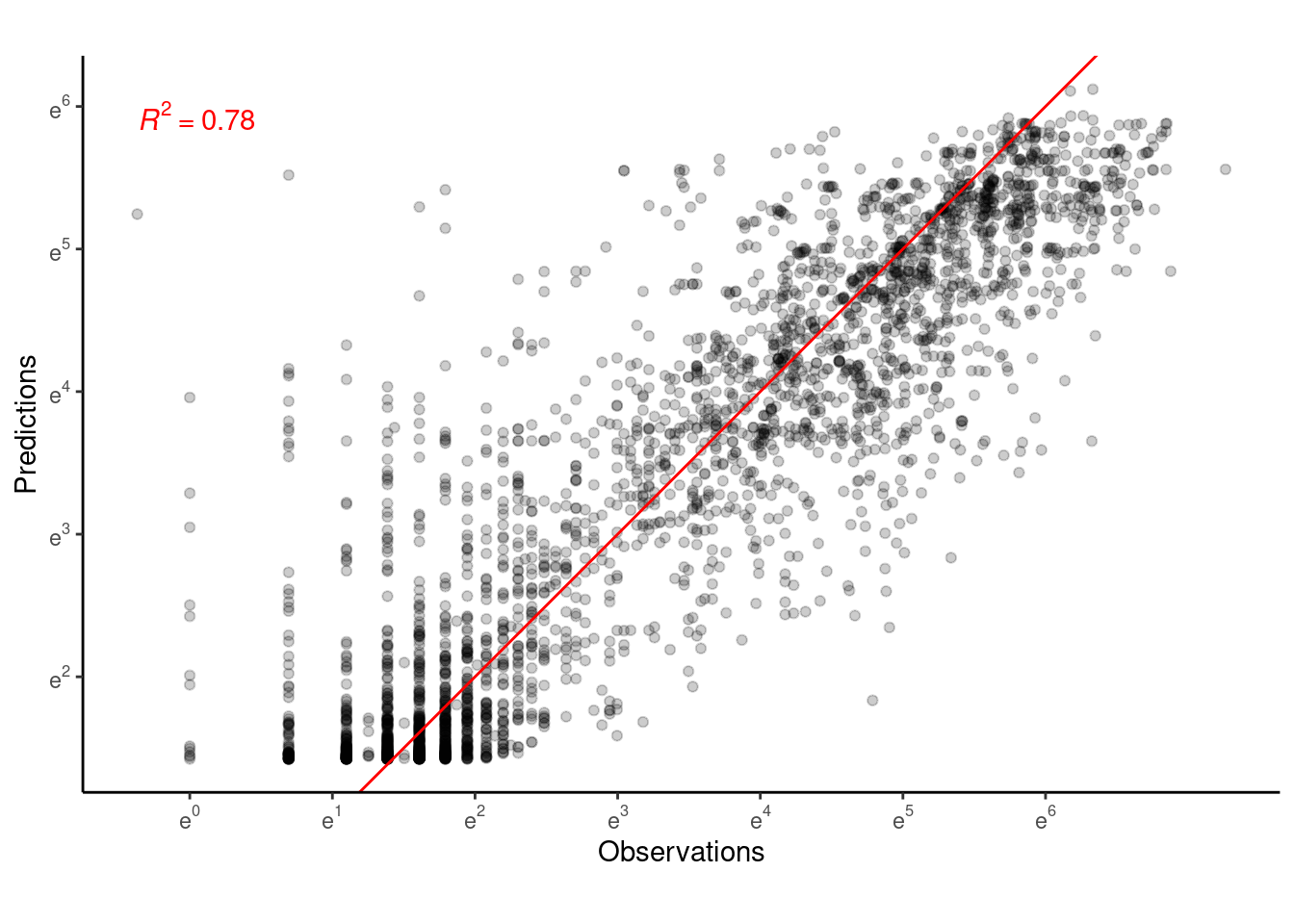
Bayesian model 6

Year-level random effects. Ignore shoot-level differences. Treatments as covariates.

Model

Data model

\begin{align*} y_{i,t,d} \sim \text{Lognormal}(\mu_{i,t,d}, \sigma^2) \end{align*}

Process model

\begin{align*} \mu_{i,t,d} &= c+\frac{A_{i,t}}{1+e^{-k_{i,t}(d-x_{0 i,t})}} \newline A_{i,t} &= \mu_A + \delta_{A,i}+ \alpha_{A,t} \newline x_{0 i,t} &= \mu_{x_0} + \delta_{x_0,i}+ \alpha_{x_0,t} \newline log(k_{i,t}) &= \mu_{log(k)} + \delta_{log(k),i}+ \alpha_{log(k),t} \end{align*}

Fixed effects

Random effects

\begin{align*} \alpha_{A,t} &\sim \text{Normal}(0, \sigma_A^2) \newline \alpha_{x_0,t} &\sim \text{Normal}(0, \sigma_{x_0}^2) \newline \alpha_{log(k),t} &\sim \text{Normal}(0, \sigma_{log(k)}^2) \end{align*}

Priors

c &\sim \text{Normal}(0, 1) \newline \begin{align*} \mu_A &\sim \text{Normal}(5, 1) \newline \beta_A &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 1 & 0 & 0 \newline 0 & 1 & 0 \newline 0 & 0 & 1 \newline \end{pmatrix} )\newline \sigma_A^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \newline \mu_{x_0} &\sim \text{Normal}(160, 100) \newline \beta_{x_0} &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 100 & 0 & 0 \newline 0 & 100 & 0 \newline 0 & 0 & 100 \newline \end{pmatrix} )\newline \sigma_{x_0}^2 &\sim \text{Truncated Normal}(0, 100, 0, \infty) \newline \mu_{log(k)} &\sim \text{Normal}(-2, 0.04) \newline \beta_{log(k)} &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 0.04 & 0 & 0 \newline 0 & 0.04 & 0 \newline 0 & 0 & 0.04 \newline \end{pmatrix} )\newline \sigma_{log(k)}^2 &\sim \text{Truncated Normal}(0, 0.04, 0, \infty) \newline \sigma^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \end{align*}

Prepare data

dat_6 <- dat_shoot_cov %>%
  filter(species == "queru", canopy == "open", site == "cfc") %>%
  filter(shoot > 0) %>%
  drop_na(barcode) %>%
  mutate(slot = if_else(is.na(slot), "", slot)) %>%
  mutate(group = year %>% factor() %>% as.integer()) %>%
  mutate(heat_trt = factor(heat_name, levels = c("ambient", "+1.7C", "+3.4C"), labels = c(0, 1, 2)) %>% as.character() %>% as.integer()) %>%
  mutate(water_trt = factor(water_name, levels = c("ambient", "reduced"), labels = c(0, 1)) %>% as.character() %>% as.integer())

Fit model

df_MCMC_6 <- calc_bayes_fit(
  data = dat_6 %>% mutate(tag = "training"),
  version = 6
)
write_rds(df_MCMC_6, "alldata/intermediate/shootmodeling/df_MCMC_6.rds")

df_MCMC_6 <- read_rds("alldata/intermediate/shootmodeling/df_MCMC_6.rds") %>% tidy_mcmc(dat_6)
p_bayes_diagnostics <- plot_bayes_diagnostics(df_MCMC = df_MCMC_6, plot_corr = F)
p_bayes_diagnostics$p_MCMC

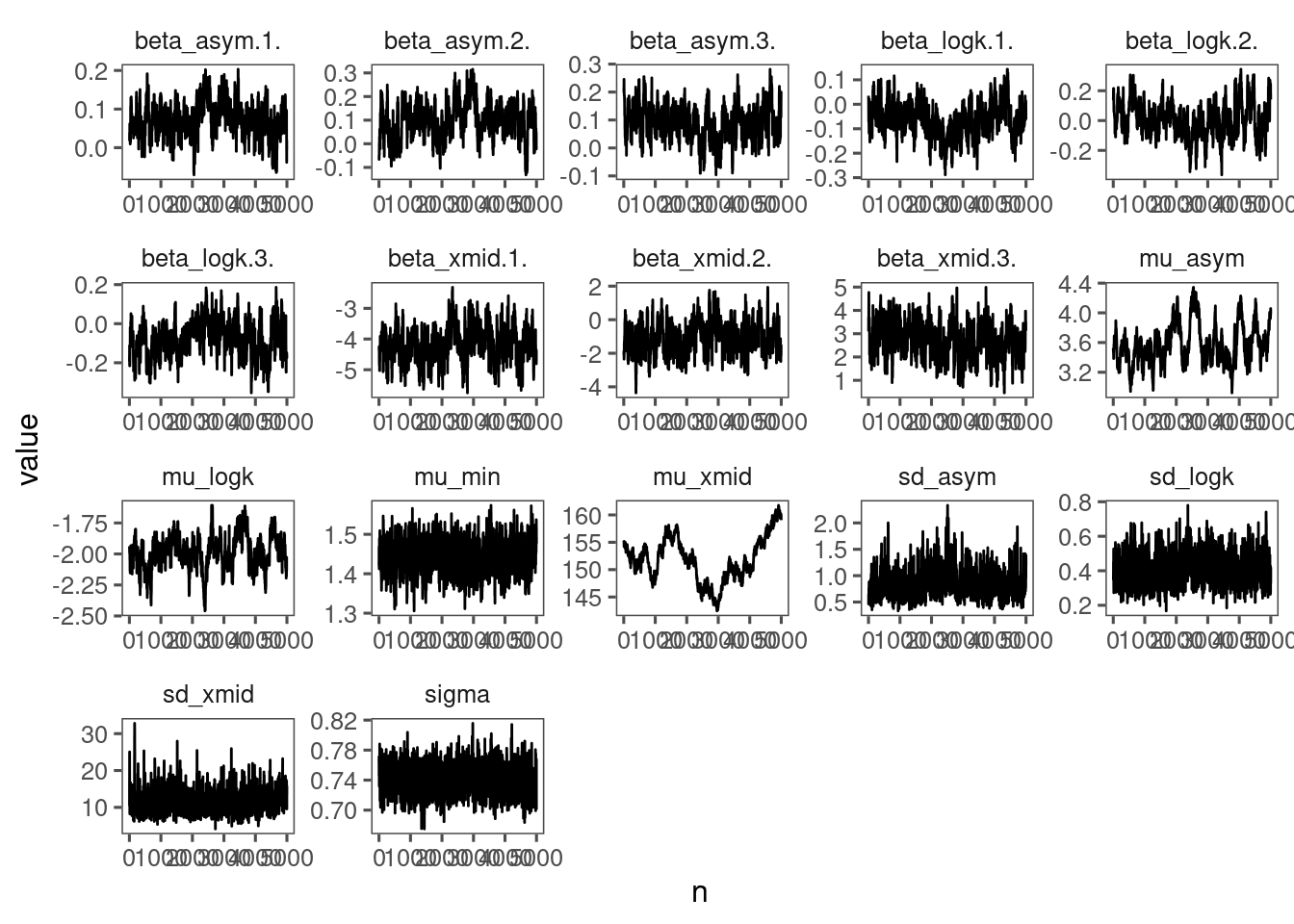
p_bayes_diagnostics$p_posterior

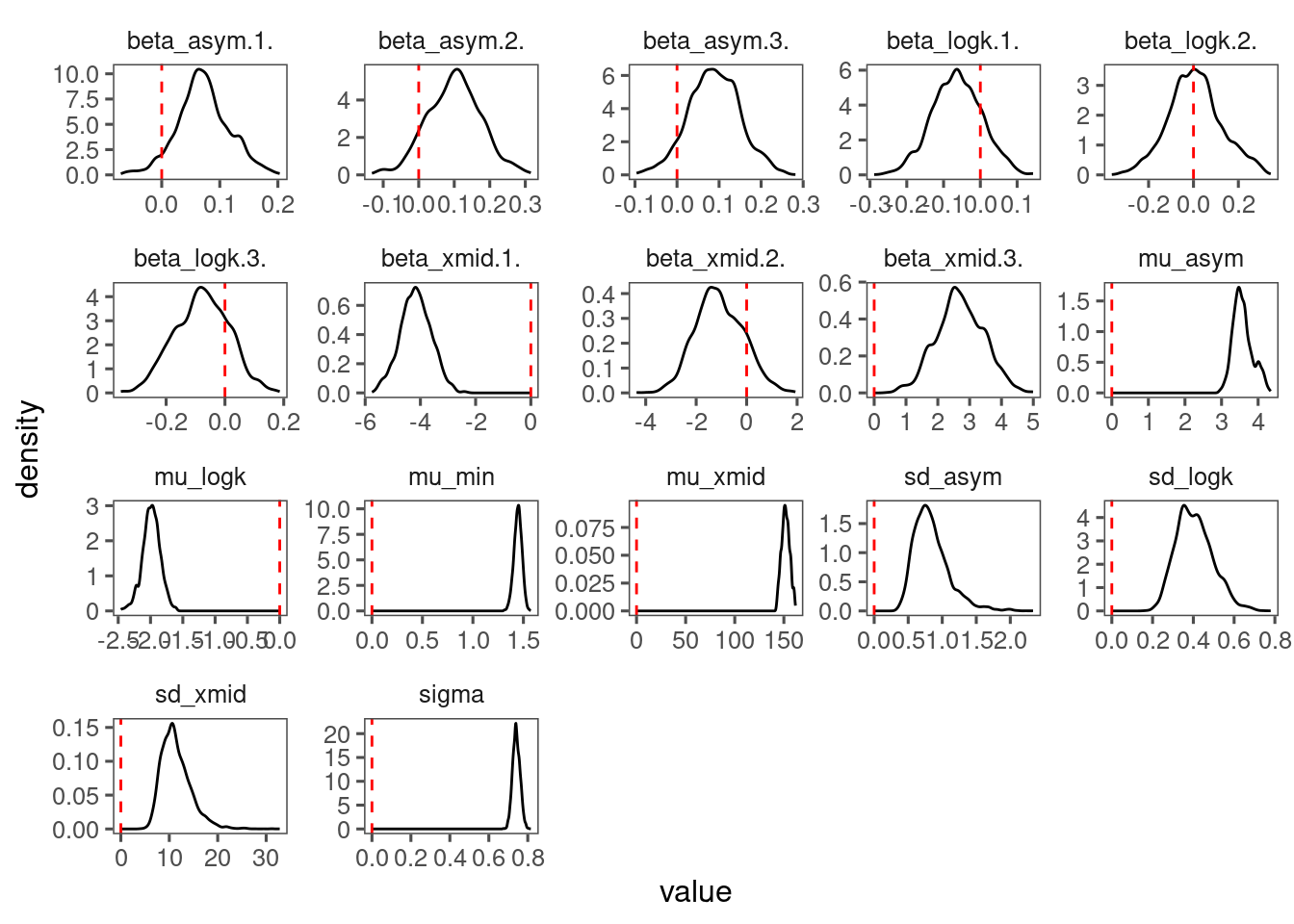
p_bayes_diagnostics$p_coefficient

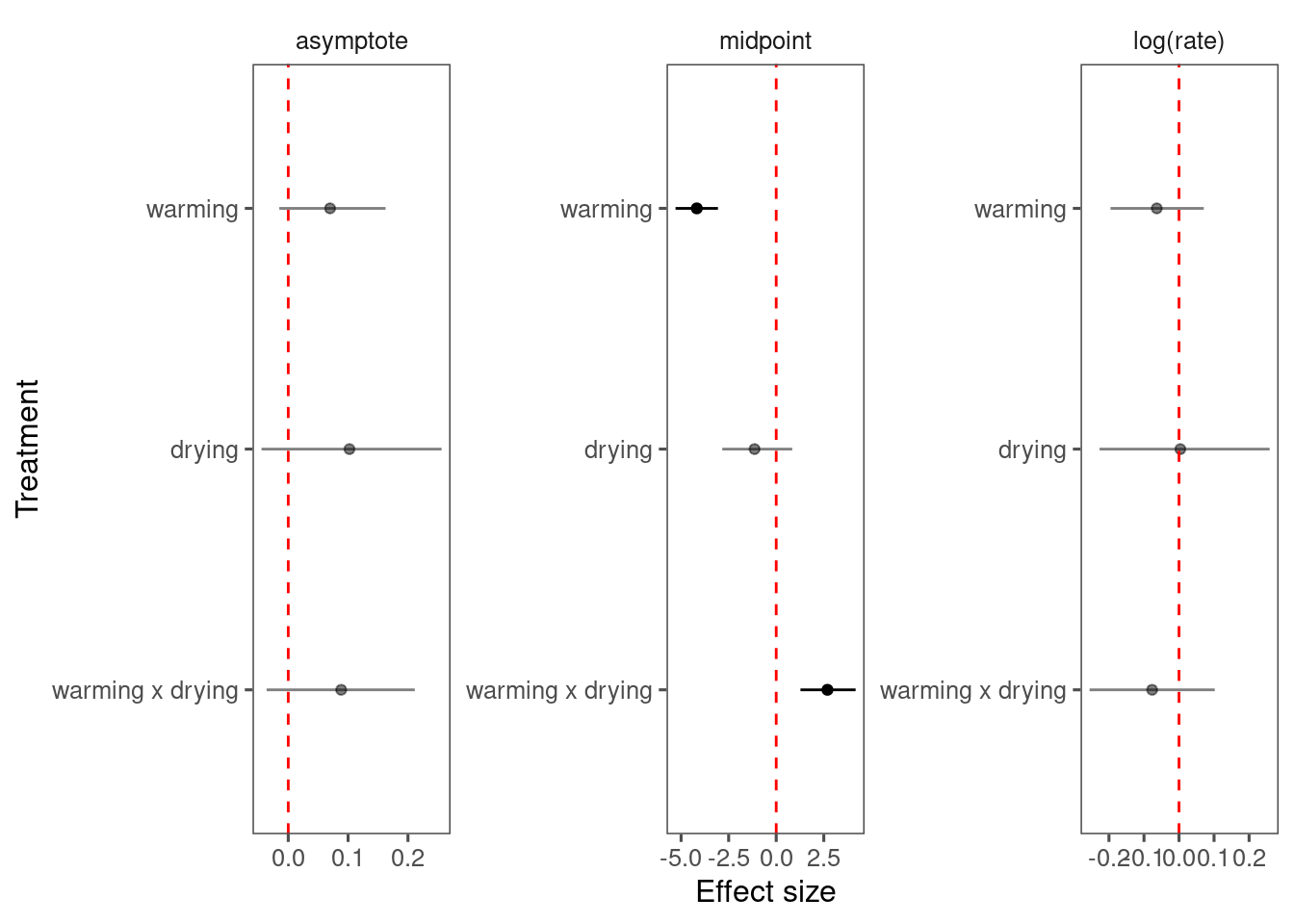
Mixing is way better than Model 4 and Model 5.

Make predictions

df_pred_6 <- calc_bayes_predict(
  data = dat_6 %>%
    distinct(year, group, heat_trt, water_trt, doy),
  df_MCMC = df_MCMC_6,
  version = 6
)
write_rds(df_pred_6, "alldata/intermediate/shootmodeling/df_pred_6.rds")

df_pred_6 <- read_rds("alldata/intermediate/shootmodeling/df_pred_6.rds")
p_bayes_predict <- plot_bayes_predict(
  data = dat_6,
  data_predict = df_pred_6,
  vis_log = T
)

p_bayes_predict$p_original

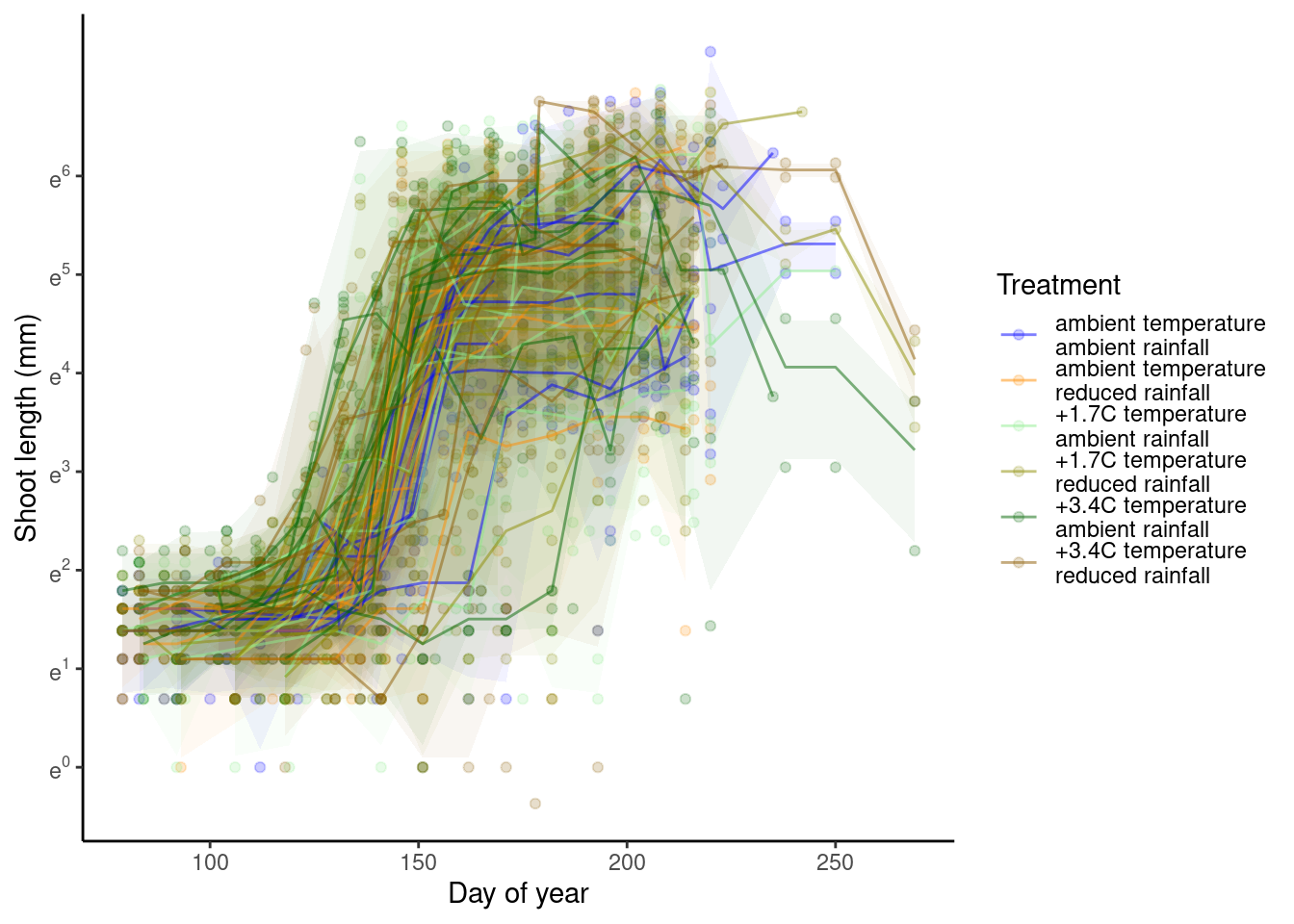
p_bayes_predict$p_overlay

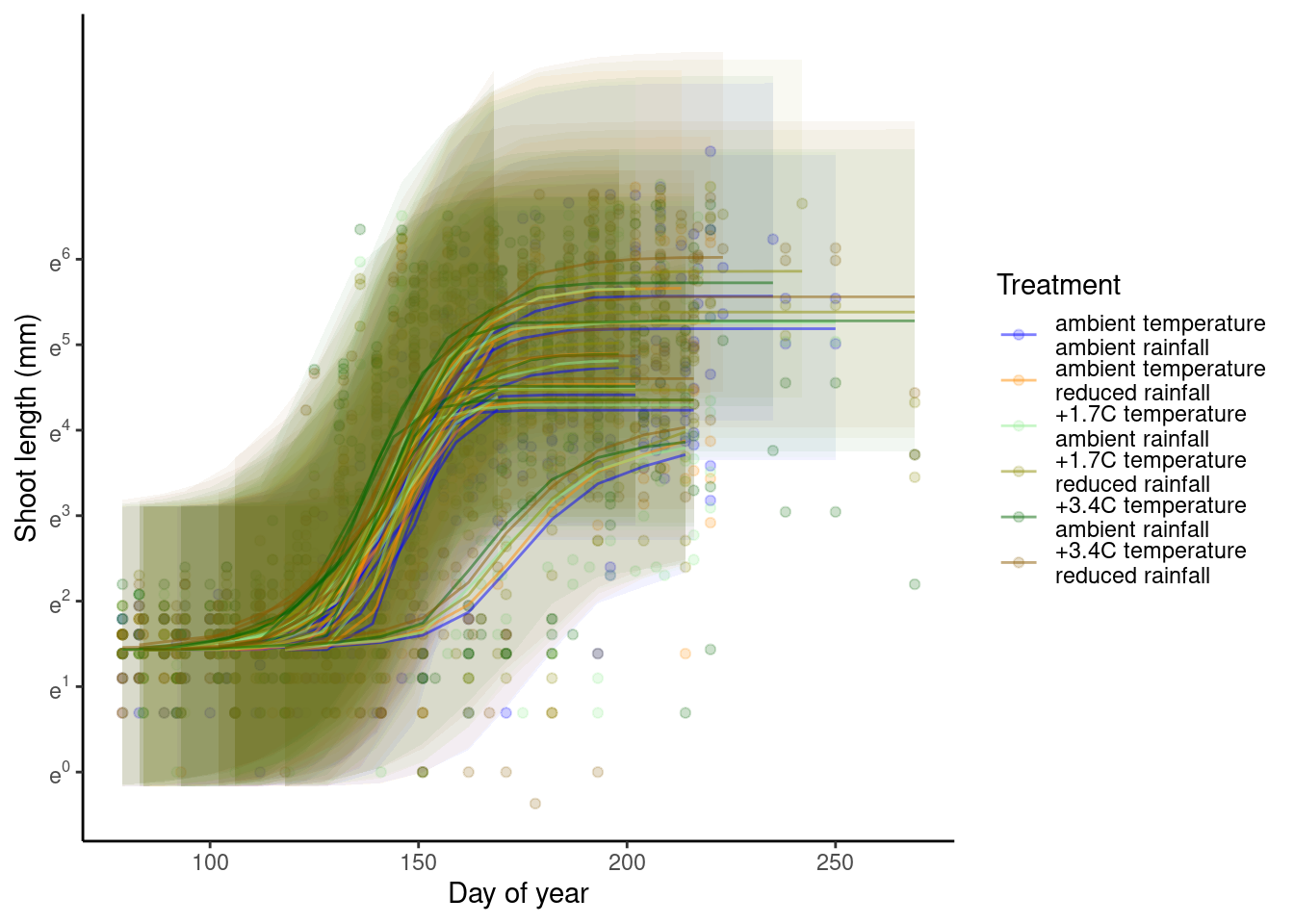
p_bayes_predict$p_accuracy

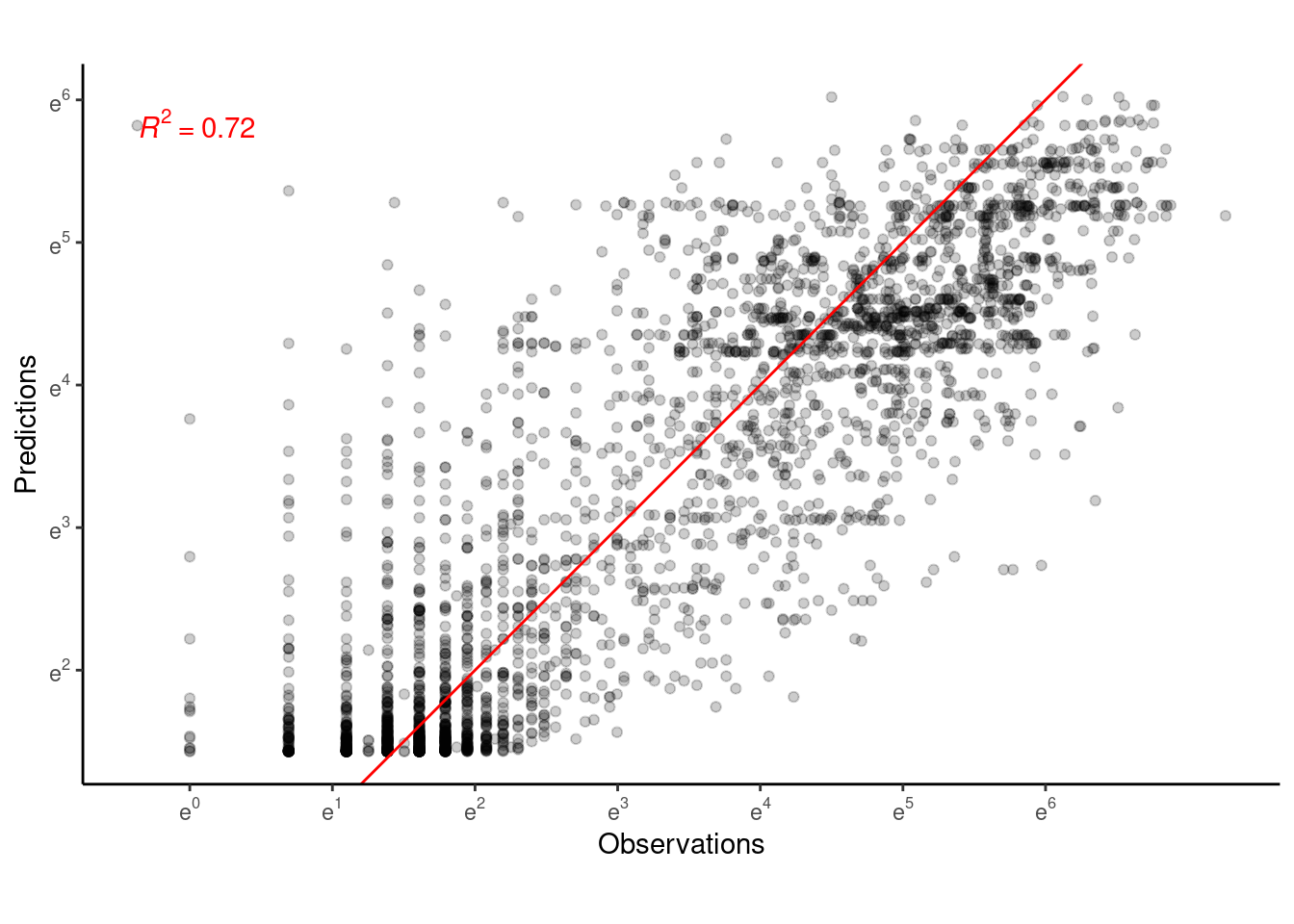
Prediction is not much worse than Model 5.

p_bayes_predict <- plot_bayes_predict(
  data = dat_6 %>% filter(year == 2013),
  data_predict = df_pred_6 %>% filter(year == 2013),
  vis_log = T
)
p_bayes_predict$p_original

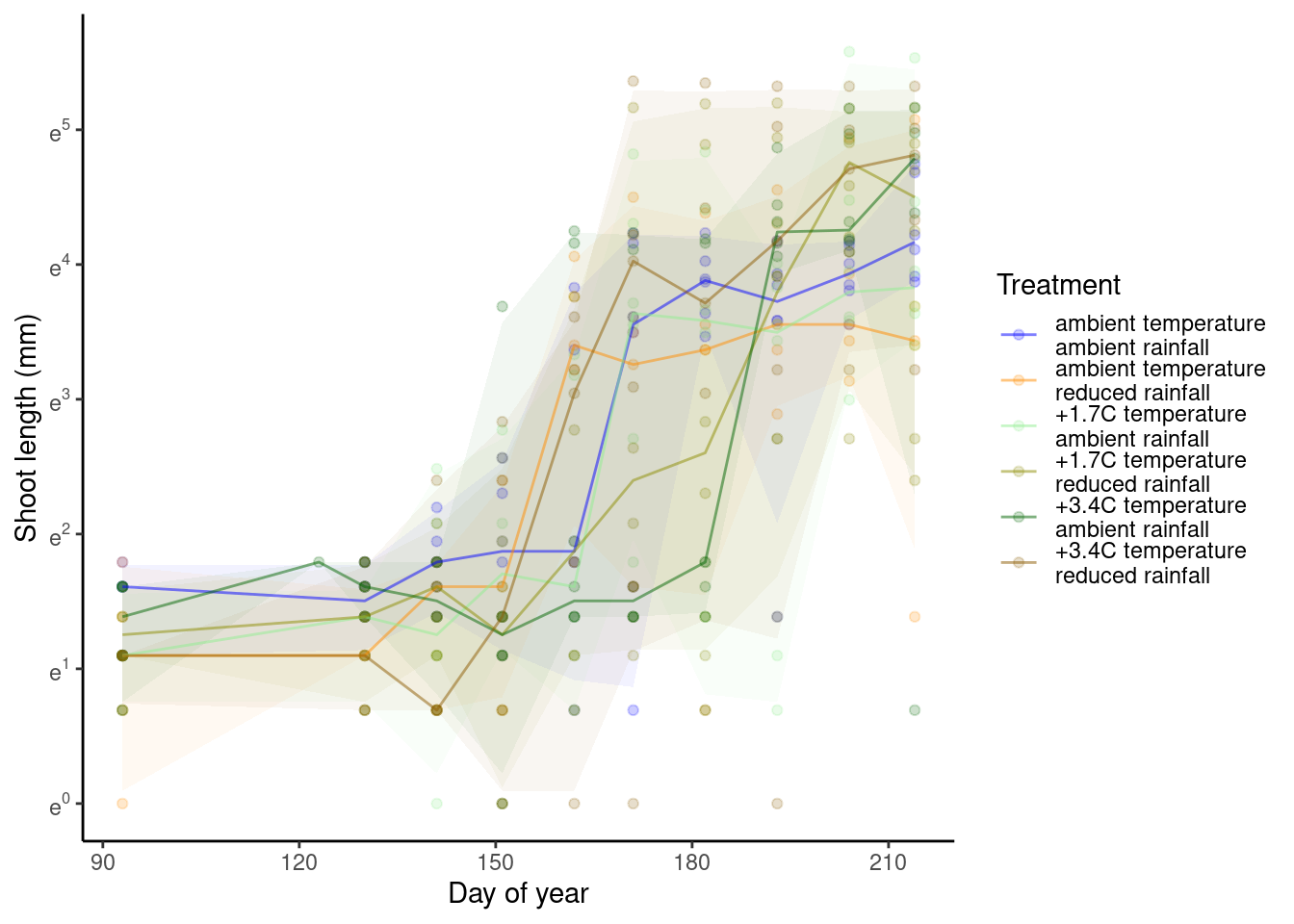
p_bayes_predict$p_overlay

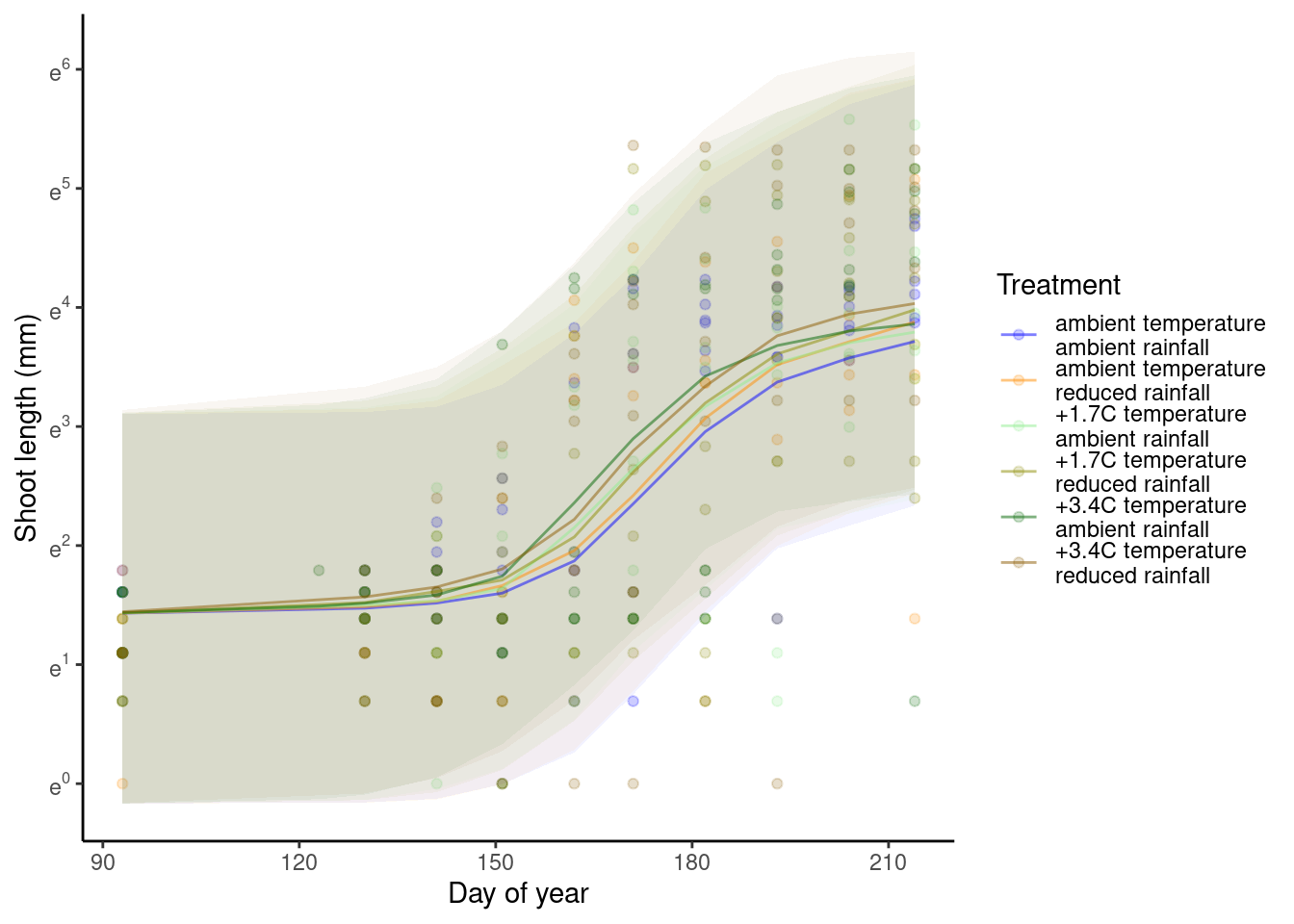Note that the effects of treatments might be reversed in year 2013, which are not captured by the current model.

If you wonder if this is because 2013 was a particularly cold year. I checked that it was colder than others, but it was similar to 2014, which did not have the reversal in treatment effect.

dat_climate_spring <- summ_climate_season(dat_climate_daily, date_start = "Mar 15", date_end = "May 15", rainfall = 1)
dat_climate_spring %>%
  ggplot() +
  geom_point(aes(x = year, y = temp))

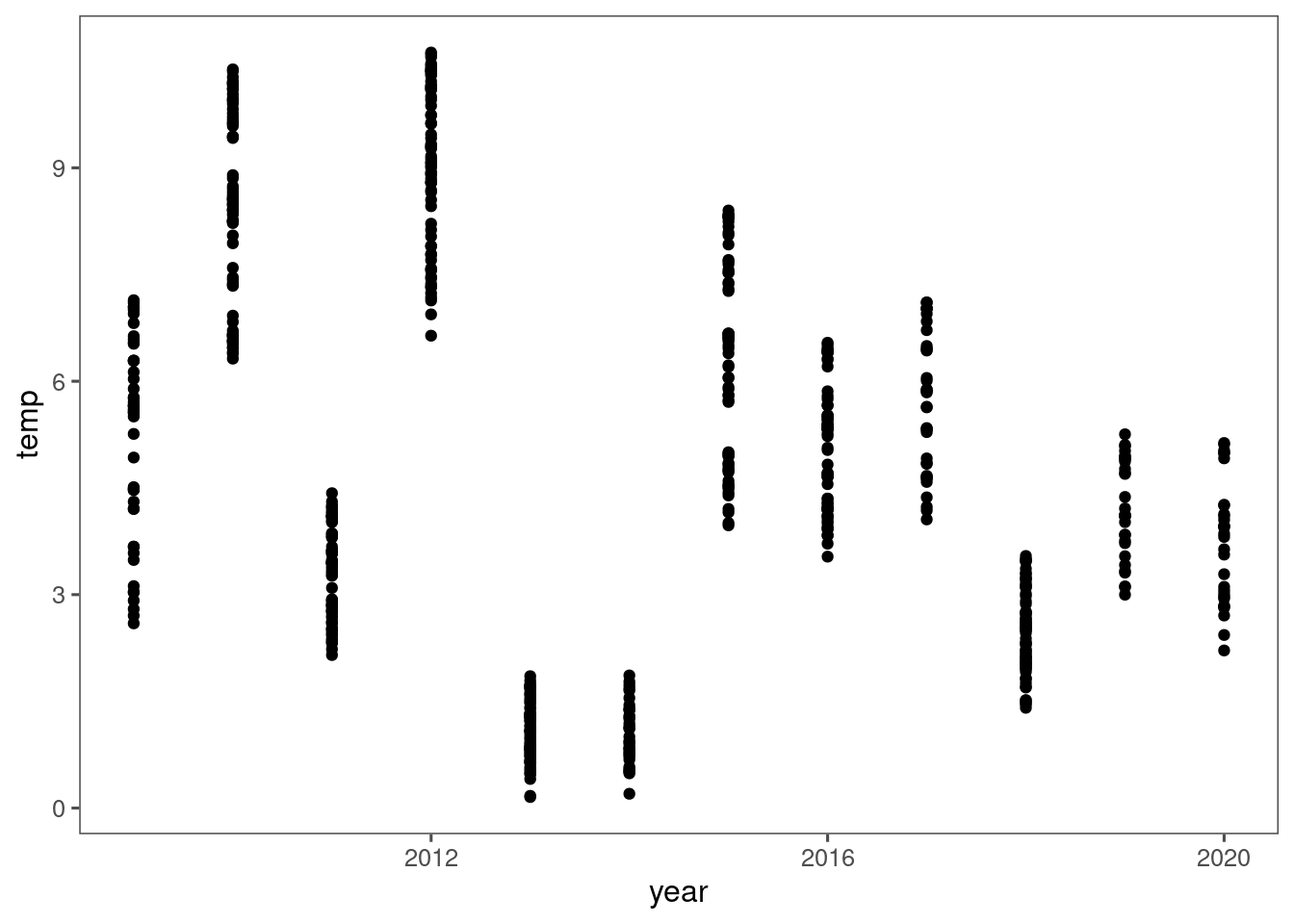Therefore, I remind us that the inference from this Bayesian model represent an overall effect, which may not be the case for individual years.

Bayesian model 7

Shoot-level random effects plus year-level random effects. Treatments as covariates.

Model

Data model

\begin{align*} y_{i,t,d} \sim \text{Lognormal}(\mu_{i,t,d}, \sigma^2) \end{align*}

Process model

\begin{align*} \mu_{i,t,d} &= c+\frac{A_{i,t}}{1+e^{-k_{i,t}(d-x_{0 i,t})}} \newline A_{i,t} &= \mu_A + \delta_{A,i}+ \alpha_{A,i} + \gamma_{A, t}\newline x_{0 i,t} &= \mu_{x_0} + \delta_{x_0,i}+ \alpha_{x_0,i} + \gamma_{x_0,t} \newline log(k_{i,t}) &= \mu_{log(k)} + \delta_{log(k),i}+ \alpha_{log(k),i} + \gamma_{log(k),t} \end{align*}

Fixed effects

Random effects

\begin{align*} \alpha_{A,i} &\sim \text{Normal}(0, \sigma_{A,\alpha}^2) \newline \alpha_{x_0,i} &\sim \text{Normal}(0, \sigma_{x_0,\alpha}^2) \newline \alpha_{log(k),i} &\sim \text{Normal}(0, \sigma_{log(k),\alpha}^2) \newline

\gamma_{A,t} &\sim \text{Normal}(0, \sigma_{A,\gamma}^2) \newline \gamma_{x_0,t} &\sim \text{Normal}(0, \sigma_{x_0,\gamma}^2) \newline \gamma_{log(k),t} &\sim \text{Normal}(0, \sigma_{log(k),\gamma}^2) \end{align*}

Priors

\begin{align*} c &\sim \text{Normal}(0, 1) \newline \mu_A &\sim \text{Normal}(5, 1) \newline \beta_A &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 1 & 0 & 0 \newline 0 & 1 & 0 \newline 0 & 0 & 1 \newline \end{pmatrix} )\newline \sigma_{A,\alpha}^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \newline \sigma_{A,\gamma}^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \newline \mu_{x_0} &\sim \text{Normal}(160, 100) \newline \beta_{x_0} &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 100 & 0 & 0 \newline 0 & 100 & 0 \newline 0 & 0 & 100 \newline \end{pmatrix} )\newline \sigma_{x_0, \alpha}^2 &\sim \text{Truncated Normal}(0, 100, 0, \infty) \newline \sigma_{x_0, \gamma}^2 &\sim \text{Truncated Normal}(0, 100, 0, \infty) \newline \mu_{log(k)} &\sim \text{Normal}(-2, 0.04) \newline \beta_{log(k)} &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 0.04 & 0 & 0 \newline 0 & 0.04 & 0 \newline 0 & 0 & 0.04 \newline \end{pmatrix} )\newline \sigma_{log(k), \alpha}^2 &\sim \text{Truncated Normal}(0, 0.04, 0, \infty) \newline \sigma_{log(k), \gamma}^2 &\sim \text{Truncated Normal}(0, 0.04, 0, \infty) \newline \sigma^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \end{align*}

Prepare data

dat_7 <- dat_shoot_cov %>%
  filter(species == "queru", canopy == "open", site == "cfc") %>%
  filter(shoot > 0) %>%
  drop_na(barcode) %>%
  mutate(slot = if_else(is.na(slot), "", slot)) %>%
  mutate(group = str_c(barcode, slot, sep = "_") %>% factor() %>% as.integer()) %>%
  mutate(year_code = year %>% factor() %>% as.integer()) %>%
  mutate(heat_trt = factor(heat_name, levels = c("ambient", "+1.7C", "+3.4C"), labels = c(0, 1, 2)) %>% as.character() %>% as.integer()) %>%
  mutate(water_trt = factor(water_name, levels = c("ambient", "reduced"), labels = c(0, 1)) %>% as.character() %>% as.integer())

Fit model

df_MCMC_7 <- calc_bayes_fit(
  data = dat_7 %>% mutate(tag = "training"),
  version = 7
)
write_rds(df_MCMC_7, "alldata/intermediate/shootmodeling/df_MCMC_7.rds")

df_MCMC_7 <- read_rds("alldata/intermediate/shootmodeling/df_MCMC_7.rds") %>% tidy_mcmc(dat_7)
p_bayes_diagnostics <- plot_bayes_diagnostics(df_MCMC = df_MCMC_7, plot_corr = F)
p_bayes_diagnostics$p_MCMC

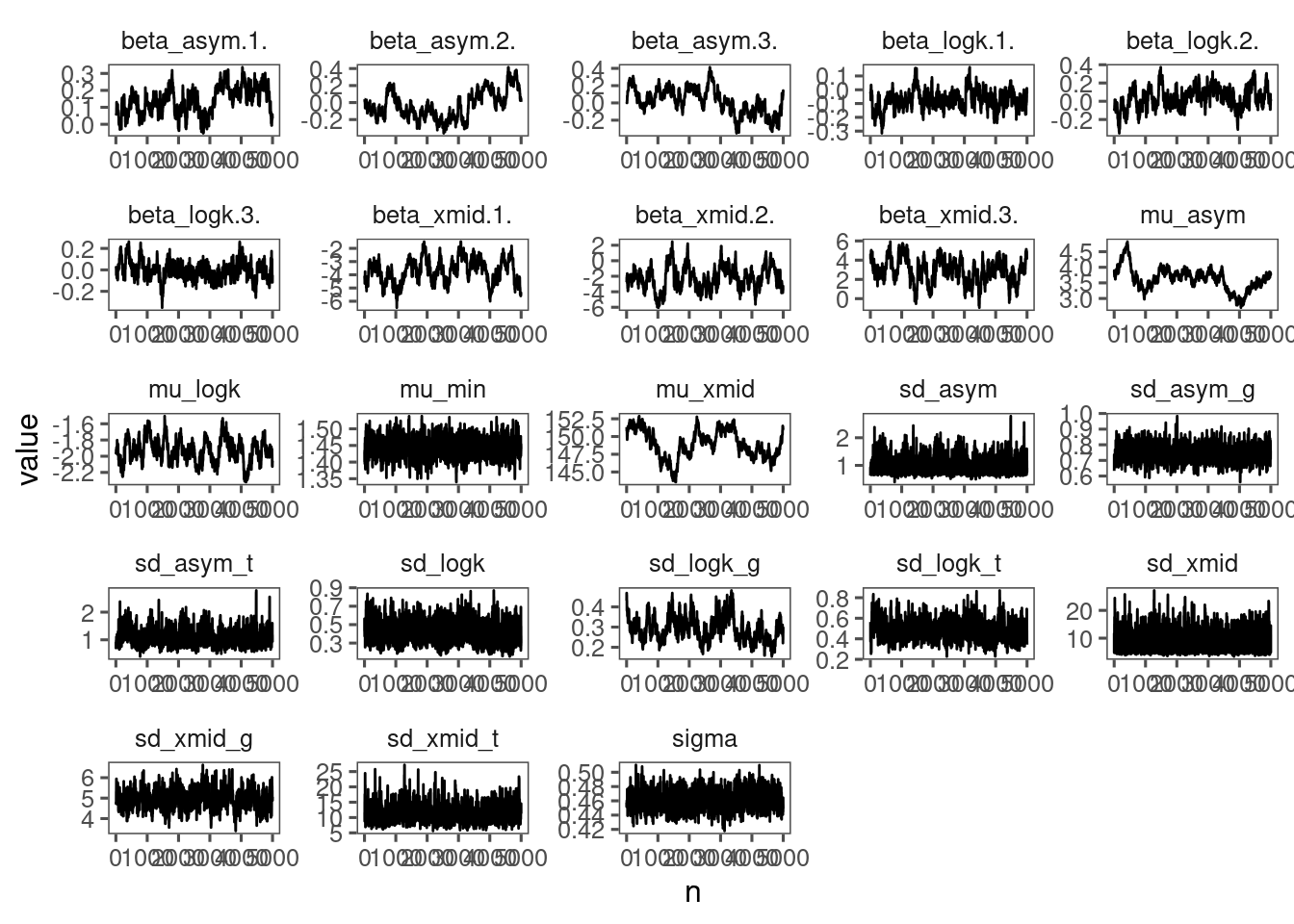
p_bayes_diagnostics$p_posterior

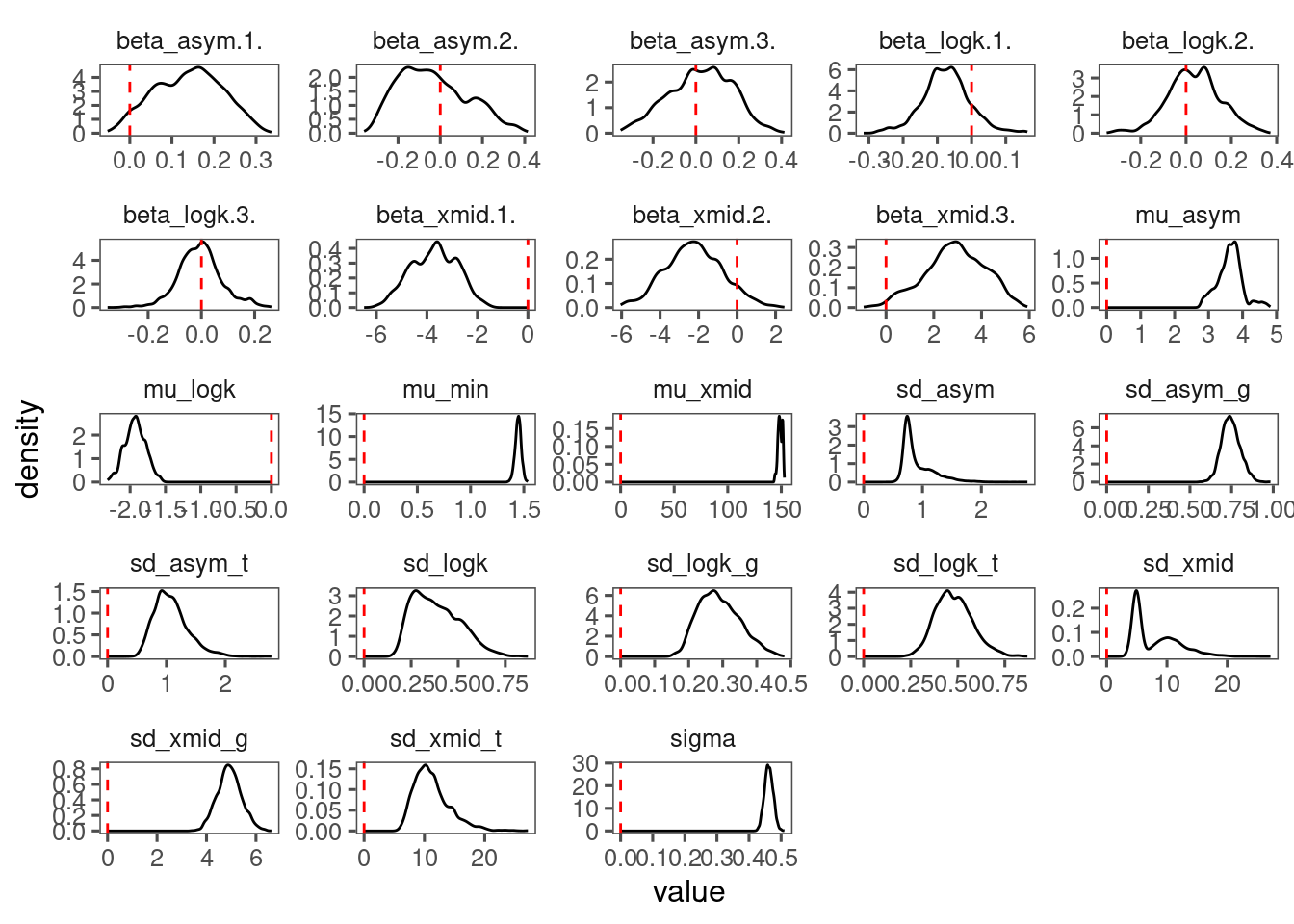
p_bayes_diagnostics$p_coefficient

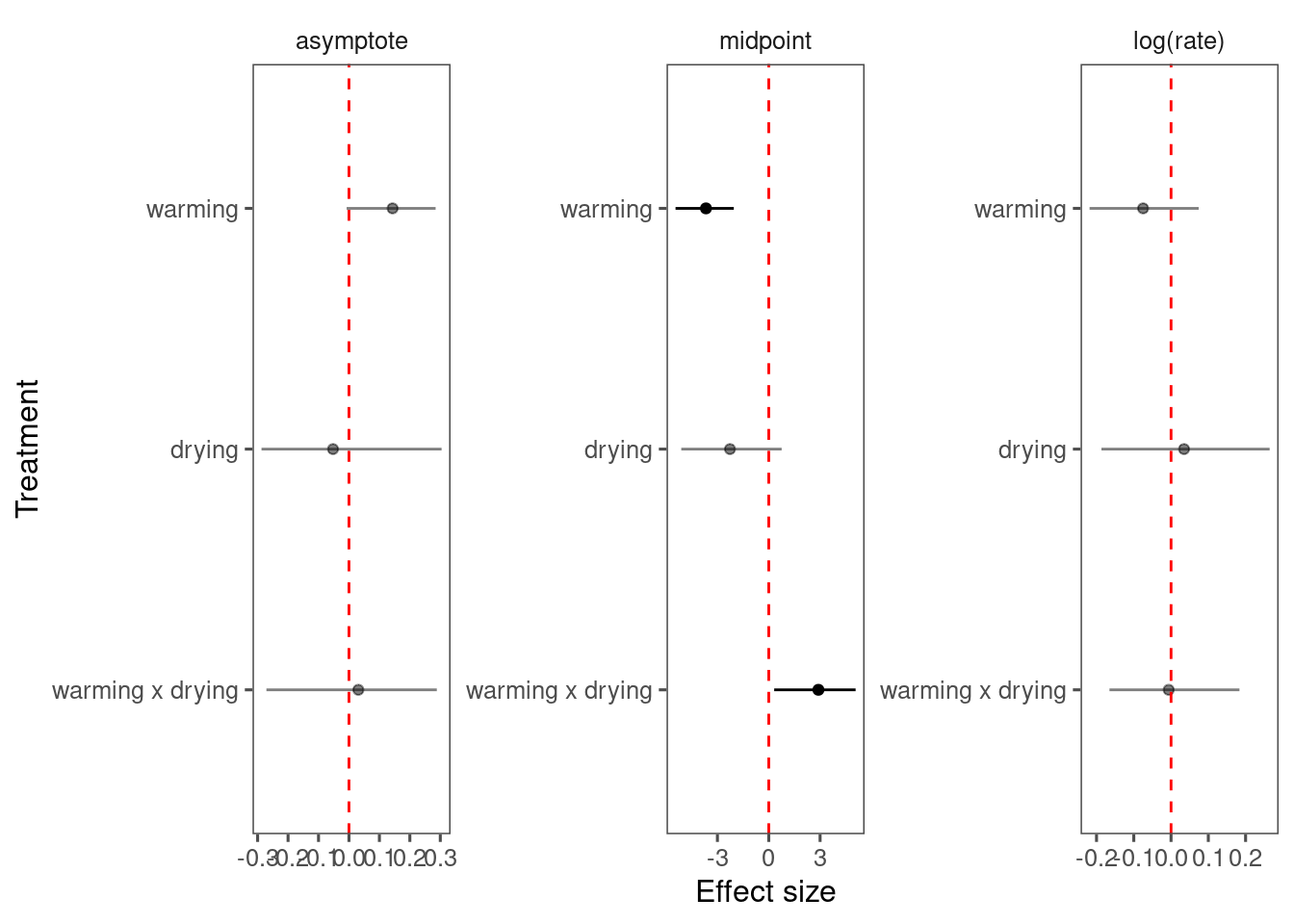
Mixing is not great. Inference similar.

Make predictions

df_pred_7 <- calc_bayes_predict(
  data = dat_7 %>%
    distinct(group, year, year_code, heat_trt, water_trt, doy),
  df_MCMC = df_MCMC_7,
  version = 7
)
write_rds(df_pred_7, "alldata/intermediate/shootmodeling/df_pred_7.rds")

df_pred_7 <- read_rds("alldata/intermediate/shootmodeling/df_pred_7.rds")
p_bayes_predict <- plot_bayes_predict(
  data = dat_7,
  data_predict = df_pred_7,
  vis_log = T
)
p_bayes_predict$p_original

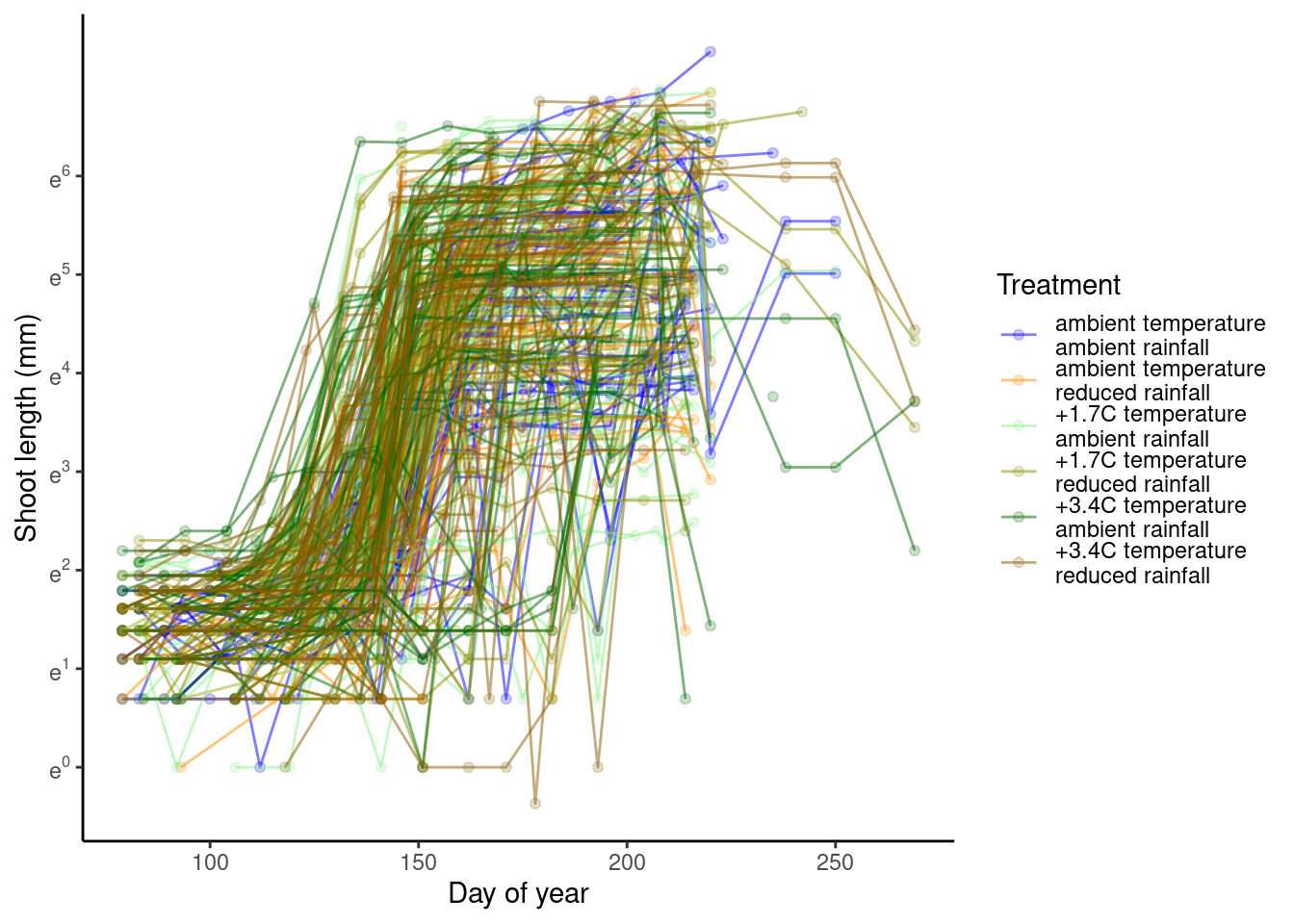
p_bayes_predict$p_overlay

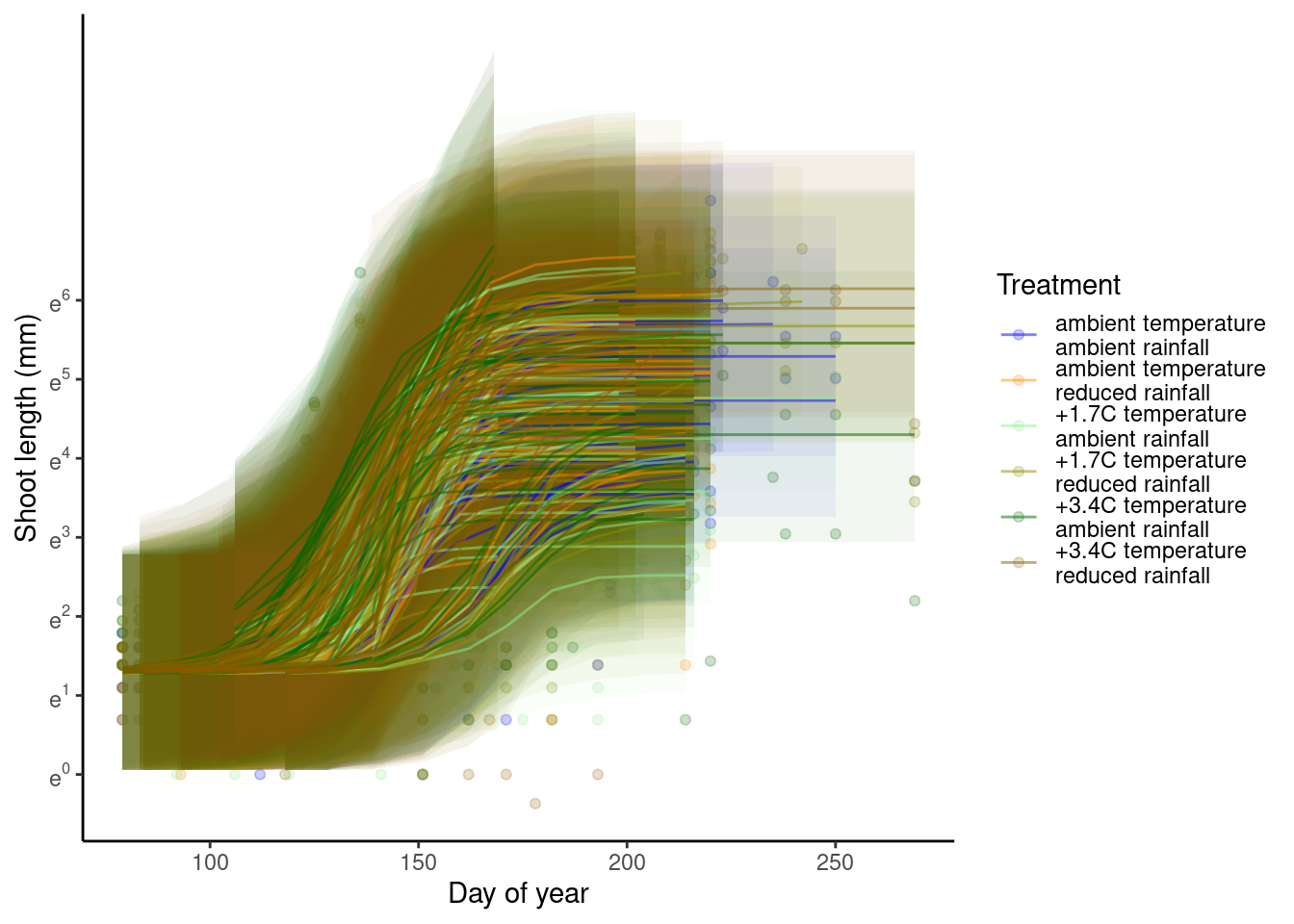
p_bayes_predict$p_accuracy

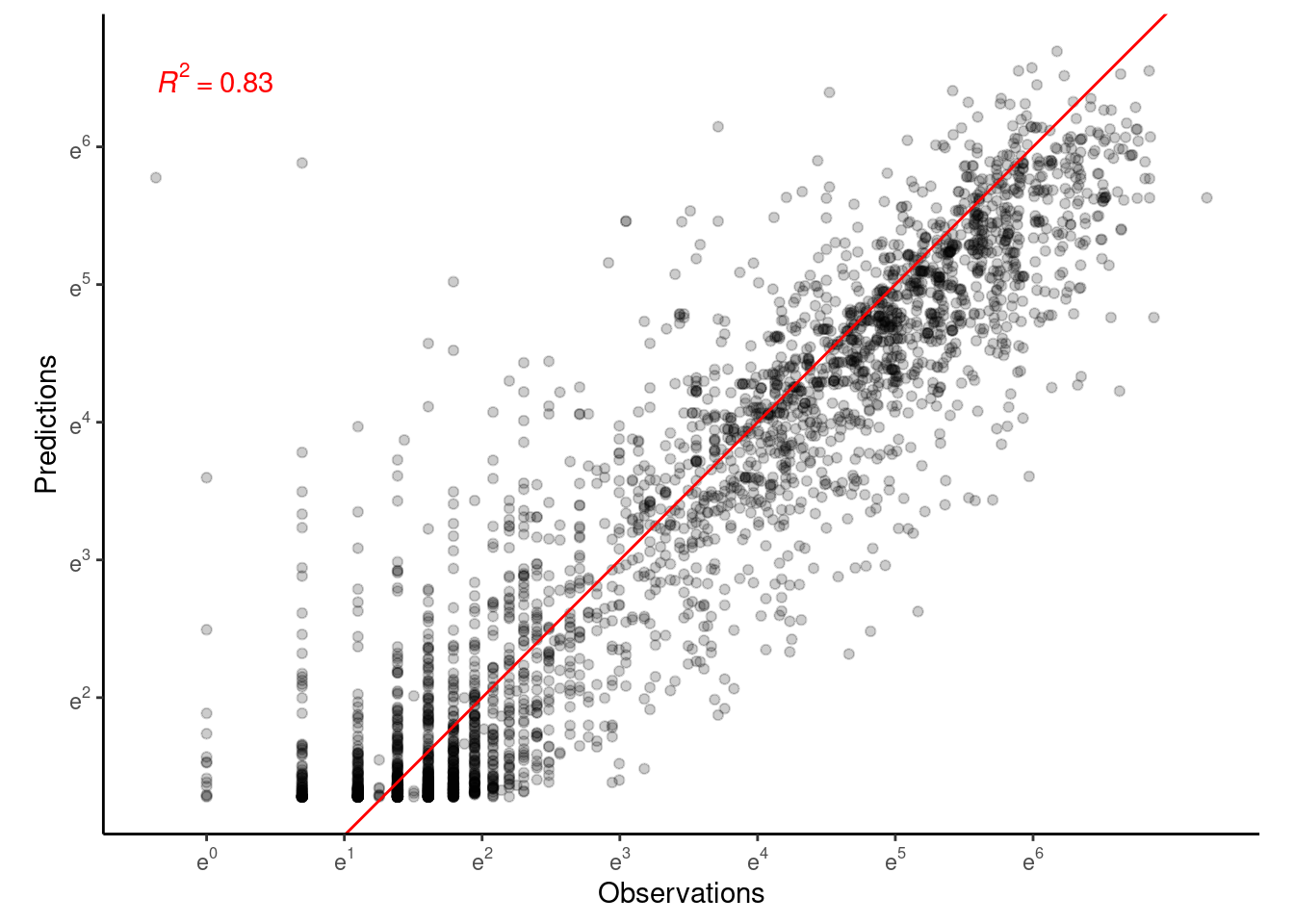
Fit not too bad compared to Model 4.

Bayesian model 8

Shoot-year-level random effects with temporally autoregressive parameters over years for each shoot. Treatments as covariates. This is written but not recommended, because I think inter-annual variations are greater than variations between shoots within a year. It might be hard to describe the effects of warm vs. cold years with temporal autoregression.

Model

Data model

\begin{align*} y_{i,t,d} \sim \text{Lognormal}(\mu_{i,t,d}, \sigma^2) \end{align*}

Process model

\begin{align*} \mu_{i,t,d} &= c+\frac{A_{i,t}}{1+e^{-k_{i}(d-x_{0 i,t})}} \newline A_{i,t} &= \mu_A + \delta_{A,i}+ \alpha_{A,i,t} \newline x_{0 i,t} &= \mu_{x_0} + \delta_{x_0, i}+ \alpha_{x_0,i,t} \newline log(k_{i,t}) &= \mu_{log(k)}+ \delta_{log(k),i}+ \alpha_{log(k),i,t} \end{align*}

Fixed effects

Random effects

\begin{align*} \alpha_{A,i,1} &\sim \text{Normal}(0, \sigma_{A,1}^2) \newline \alpha_{A,i,t} &\sim \text{Normal}(\alpha_{A,i,t-1}, \sigma_{A,t}^2) \newline \alpha_{x_0,i,1} &\sim \text{Normal}(0,\sigma_{x_0,1}^2) \newline \alpha_{x_0,i,t} &\sim \text{Normal}(\alpha_{x_0,i,t-1}, \sigma_{x_0,t}^2) \newline \alpha_{log(k),i,1} &\sim \text{Normal}(0,\sigma_{log(k),1}^2) \newline \alpha_{log(k),i,t} &\sim \text{Normal}(\alpha_{log(k),i,t-1}, \sigma_{log(k),t}^2) \end{align*}

Priors

\begin{align*} c &\sim \text{Normal}(0, 1) \newline \mu_A &\sim \text{Normal}(5, 1) \newline \beta_A &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 1 & 0 & 0 \newline 0 & 1 & 0 \newline 0 & 0 & 1 \newline \end{pmatrix} )\newline \sigma_{A,1}^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \newline \sigma_{A,t}^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \newline \mu_{x_0} &\sim \text{Normal}(160, 100) \newline \beta_{x_0} &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 100 & 0 & 0 \newline 0 & 100 & 0 \newline 0 & 0 & 100 \newline \end{pmatrix} )\newline \sigma_{x_0,1}^2 &\sim \text{Truncated Normal}(0, 100, 0, \infty) \newline \sigma_{x_0,t}^2 &\sim \text{Truncated Normal}(0, 100, 0, \infty) \newline \mu_{log(k)} &\sim \text{Normal}(-2, 0.04) \newline \beta_{log(k)} &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 0.04 & 0 & 0 \newline 0 & 0.04 & 0 \newline 0 & 0 & 0.04 \newline \end{pmatrix} )\newline \sigma_{log(k),1}^2 &\sim \text{Truncated Normal}(0, 0.04, 0, \infty) \newline \sigma_{log(k),t}^2 &\sim \text{Truncated Normal}(0, 0.04, 0, \infty) \newline \sigma^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \end{align*}

Prepare data

dat_8 <- dat_shoot_cov %>%
  filter(species == "queru", canopy == "open", site == "cfc") %>%
  filter(shoot > 0) %>%
  drop_na(barcode) %>%
  mutate(slot = if_else(is.na(slot), "", slot)) %>%
  mutate(group = str_c(barcode, slot, sep = "_") %>% factor() %>% as.integer()) %>%
  group_by(group) %>%
  mutate(year_code = year %>% factor() %>% as.integer()) %>%
  ungroup() %>%
  mutate(heat_trt = factor(heat_name, levels = c("ambient", "+1.7C", "+3.4C"), labels = c(0, 1, 2)) %>% as.character() %>% as.integer()) %>%
  mutate(water_trt = factor(water_name, levels = c("ambient", "reduced"), labels = c(0, 1)) %>% as.character() %>% as.integer())

Fit model

df_MCMC_8 <- calc_bayes_fit(
  data = dat_8 %>% mutate(tag = "training"),
  version = 8
)
write_rds(df_MCMC_8, "alldata/intermediate/shootmodeling/df_MCMC_8.rds")

df_MCMC_8 <- read_rds("alldata/intermediate/shootmodeling/df_MCMC_8.rds") %>% tidy_mcmc(dat_8)
p_bayes_diagnostics <- plot_bayes_diagnostics(df_MCMC = df_MCMC_8, plot_corr = F)
p_bayes_diagnostics$p_MCMC

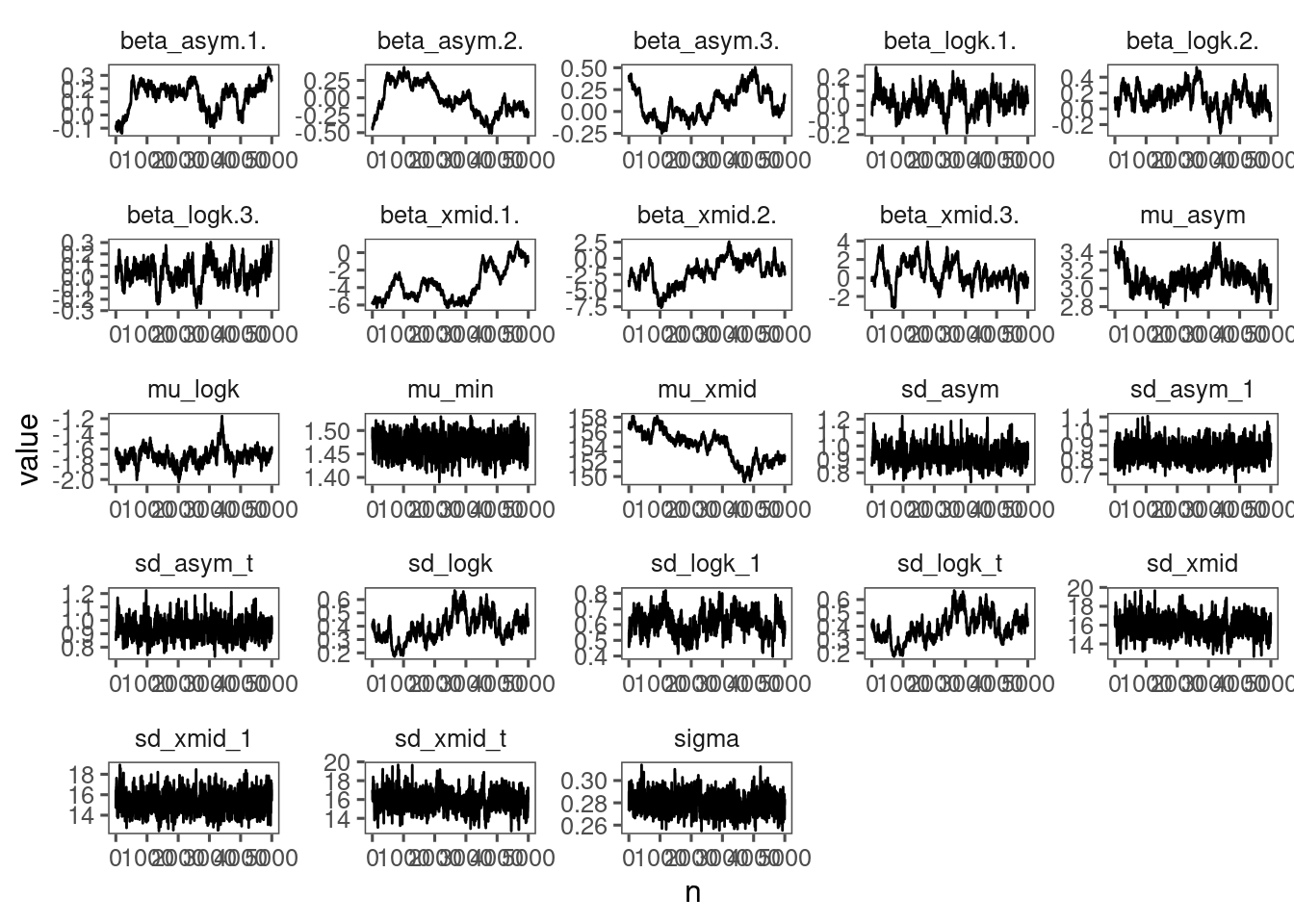
p_bayes_diagnostics$p_posterior

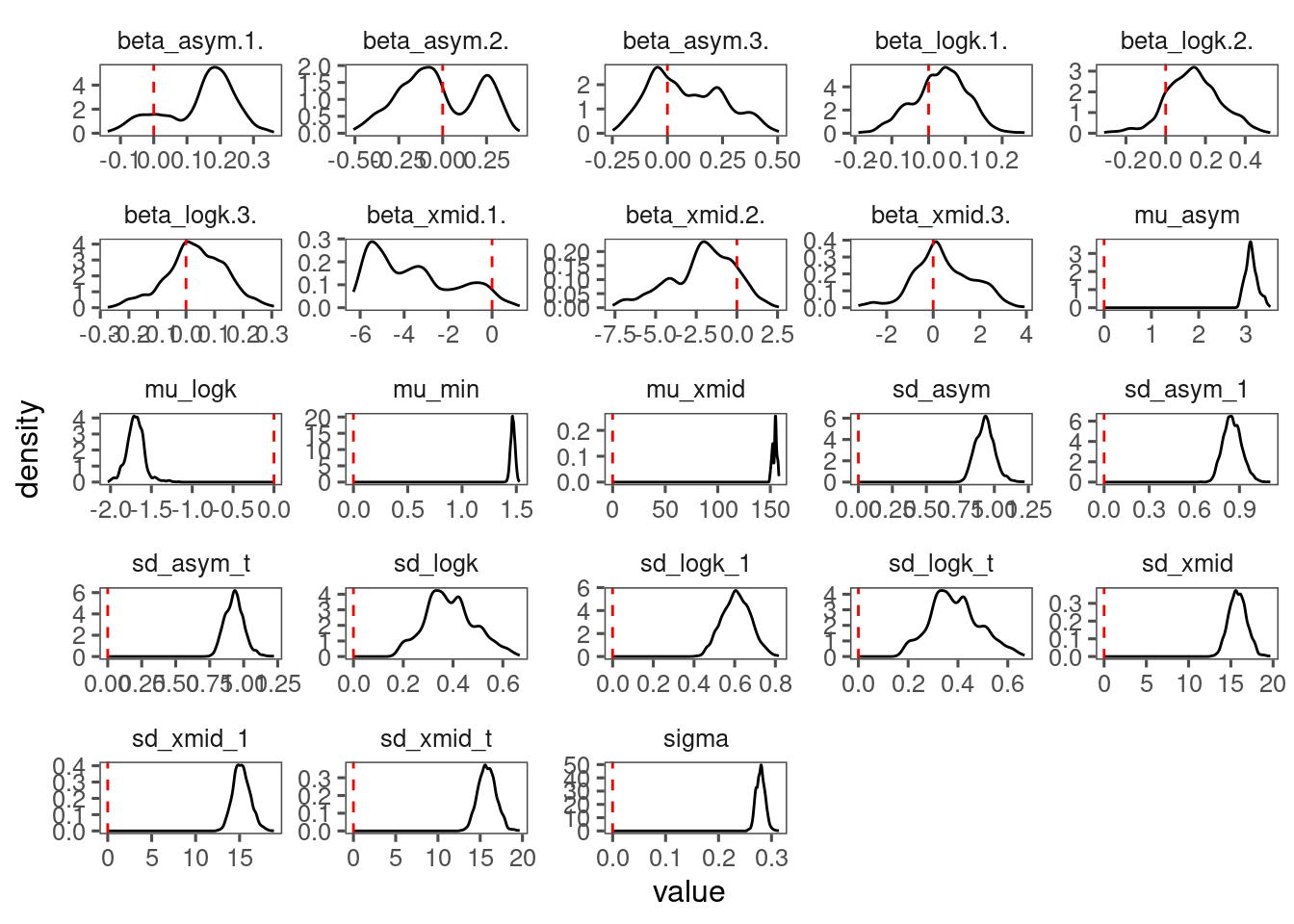
p_bayes_diagnostics$p_coefficient

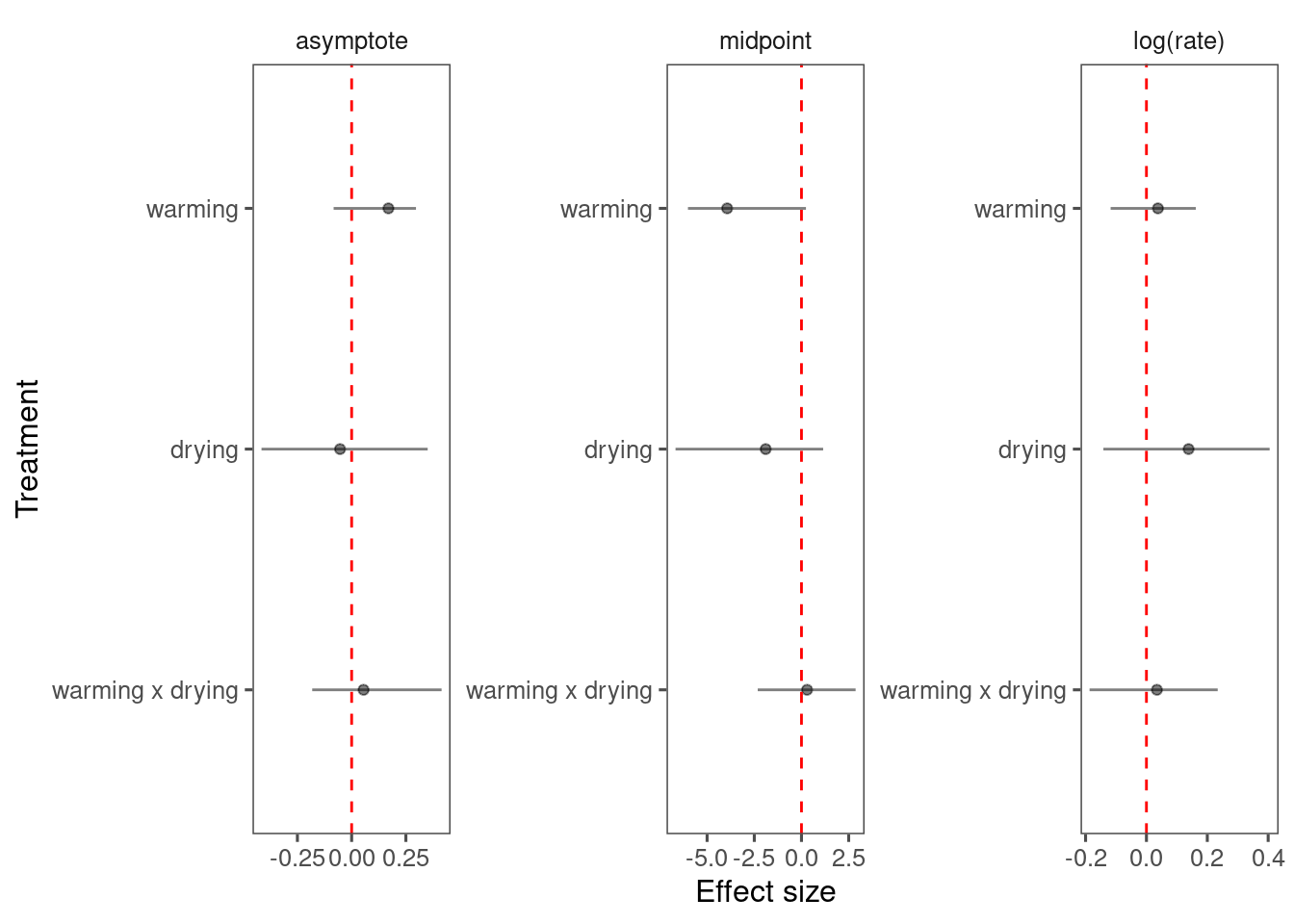Mixing is as bad as Model 4.

Make predictions

df_pred_8 <- calc_bayes_predict(
  data = dat_8 %>%
    distinct(group, year, year_code, heat_trt, water_trt, doy),
  df_MCMC = df_MCMC_8,
  version = 8
)
write_rds(df_pred_8, "alldata/intermediate/shootmodeling/df_pred_8.rds")

df_pred_8 <- read_rds("alldata/intermediate/shootmodeling/df_pred_8.rds")
p_bayes_predict <- plot_bayes_predict(
  data = dat_8,
  data_predict = df_pred_8,
  vis_log = T
)

p_bayes_predict$p_original

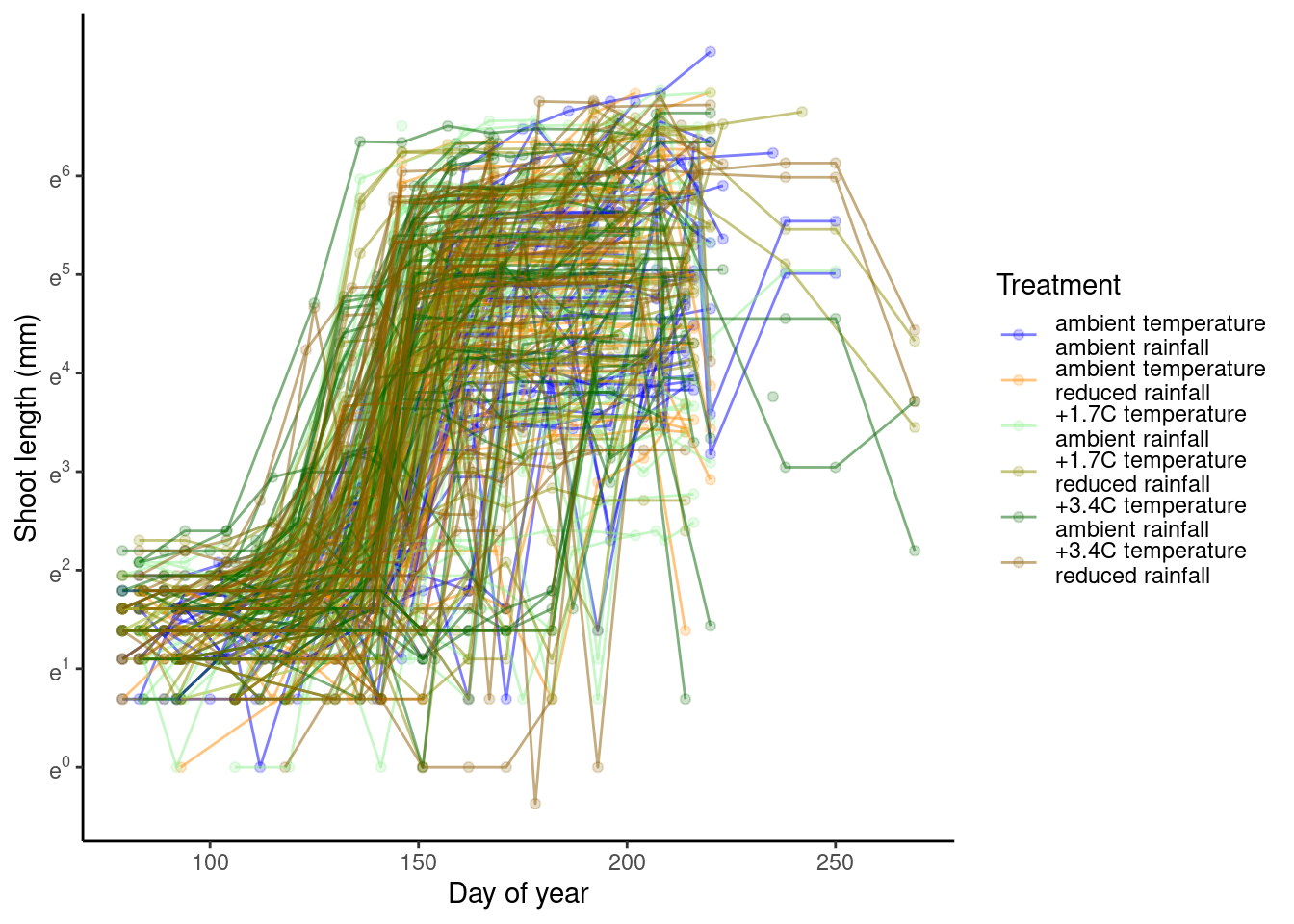
p_bayes_predict$p_overlay

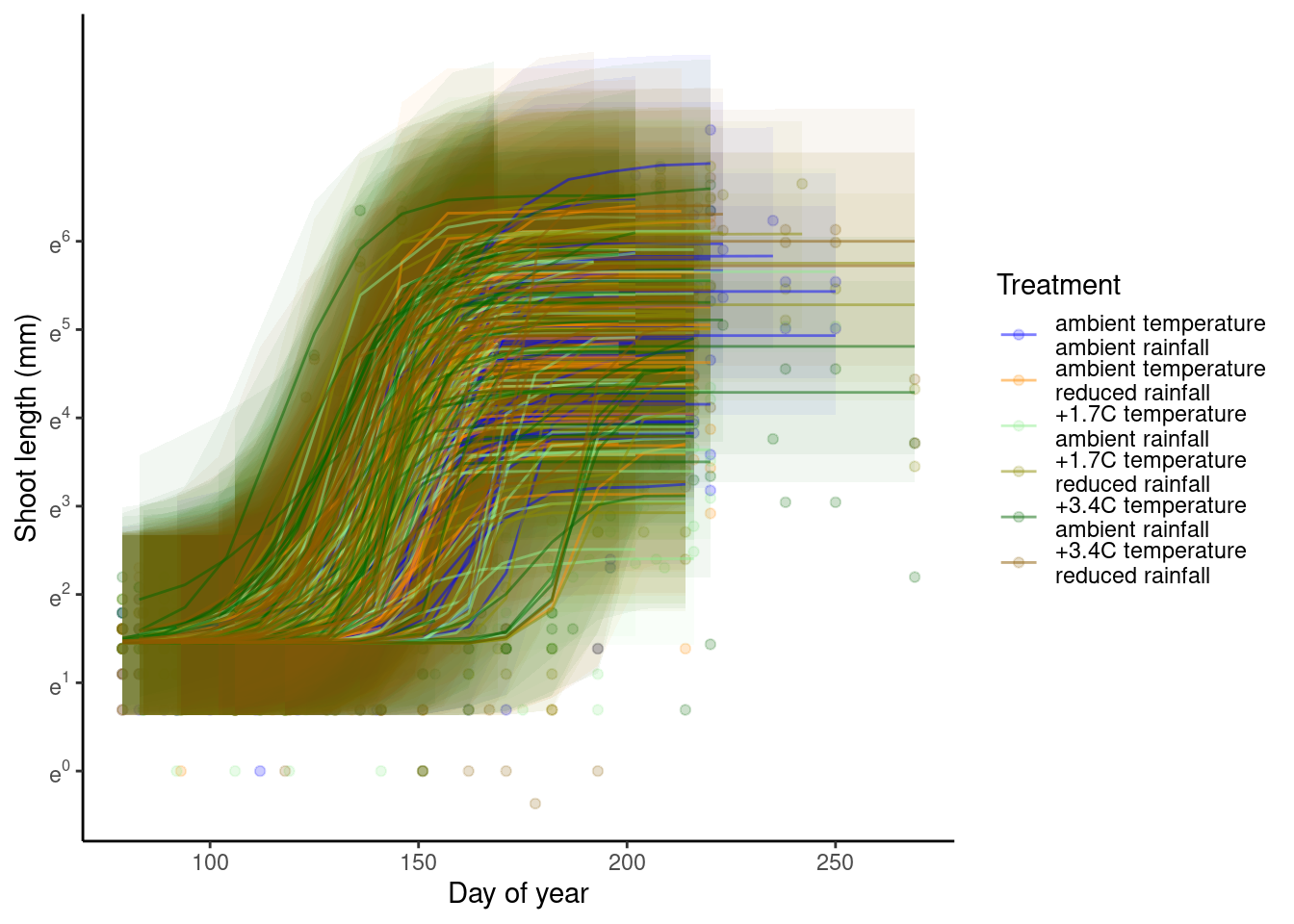
p_bayes_predict$p_accuracy

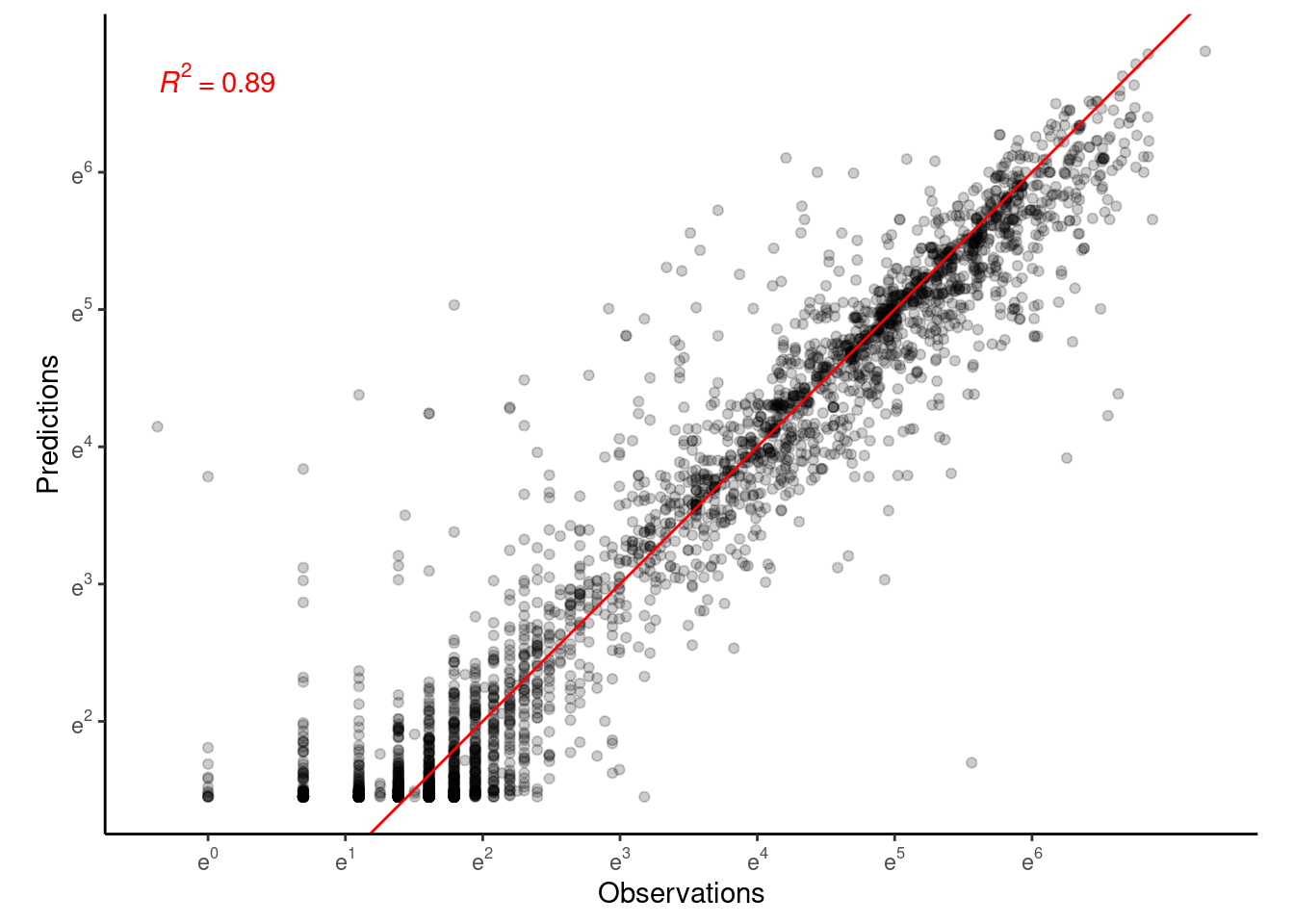Performance similar to Model 4.

Shoot growth modeling 2

Bayesian model 5

Model

Prepare data

Fit model

Make predictions

Bayesian model 6

Model

Prepare data

Fit model

Make predictions

Bayesian model 7

Model

Prepare data

Fit model

Make predictions

Bayesian model 8

Model

Prepare data

Fit model

Make predictions