Note: All analyses in this blog focus on red oak species (Quercus rubra) at the Cloquet site, open canopy conditions. If we want to expand the analyses, we have to think about how to incorporate species, site, and canopy condition into the model.
Notations
Variables
\begin{align*} y & - \text{shoot length} \newline d & - \text{day of year} \newline T = \begin{cases} 0 & \text{ambient temperature} \newline 1 & \text{+1.7°C temperature} \newline 2 & \text{+3.4°C temperature} \end{cases} & - \text{warming treatment} \newline D = \begin{cases} 0 & \text{ambient rainfall} \newline 1 & \text{reduced rainfall} \end{cases} & - \text{drought treatment} \end{align*}
Indices
\begin{align*} i &- \text{shoot (one plant can have multiple shoots)} \newline j &- \text{block (i.e., a group of closely located experimental plots)} \newline t &- \text{year} \newline d &- \text{day of year} \end{align*}
Parameters
\begin{align*} c &- \text{starting value of logistic curve} \newline A &- \text{asymptote of logistic curve} \newline x_0 &- \text{midpoint of logistic curve} \newline k &- \text{growth rate or steepness of logistic curve} \newline \sigma^2 &- \text{variance (of observation, parameters, or hyperparameters)} \end{align*}
Bayesian model 1
No random effects, no covariates.
Model
Data model
\begin{align*} y_{i,t,d} \sim \text{Lognormal}(\mu_{d}, \sigma^2) \end{align*}
Process model
\begin{align*} \mu_{d} = c+\frac{A}{1+e^{-k(d-x_0)}} \end{align*}
Priors
\begin{align*} c &\sim \text{Normal}(0, 100) \newline A &\sim \text{Normal}(5, 100) \newline x_0 &\sim \text{Normal}(160, 100) \newline log(k) &\sim \text{Normal}(-2, 0.04) \newline \sigma^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \end{align*}
Prepare data
dat_1 <- dat_shoot_cov %>%
filter(species == "queru", canopy == "open", site == "cfc") %>%
filter(shoot > 0)
Fit model
df_MCMC_1 <- calc_bayes_fit(
data = dat_1 %>% mutate(tag = "training"),
version = 1
)
write_rds(df_MCMC_1, "alldata/intermediate/shootmodeling/df_MCMC_1.rds")
df_MCMC_1 <- read_rds("alldata/intermediate/shootmodeling/df_MCMC_1.rds")
p_bayes_diagnostics <- plot_bayes_diagnostics(df_MCMC = df_MCMC_1)
p_bayes_diagnostics$p_MCMC
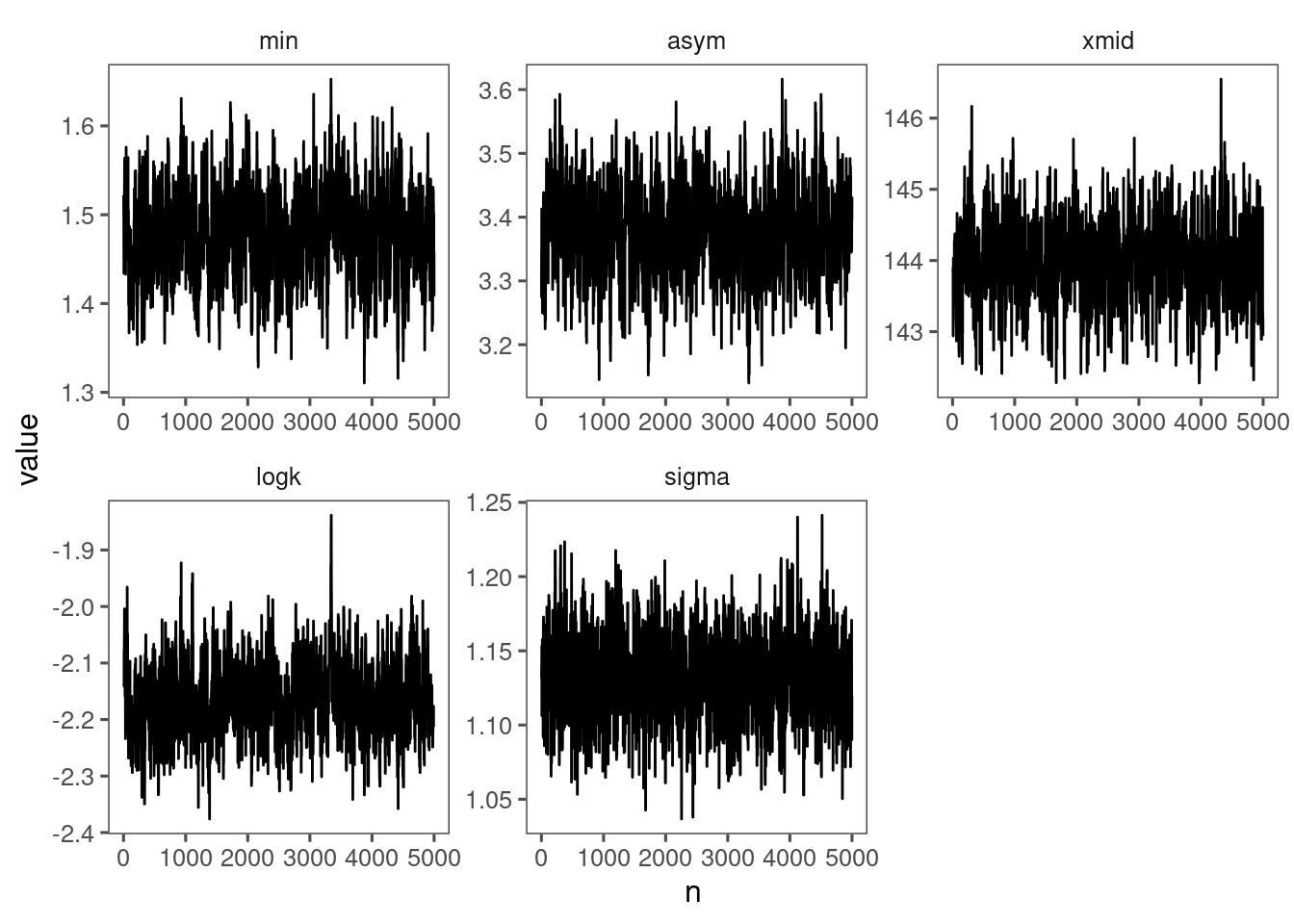
p_bayes_diagnostics$p_posterior
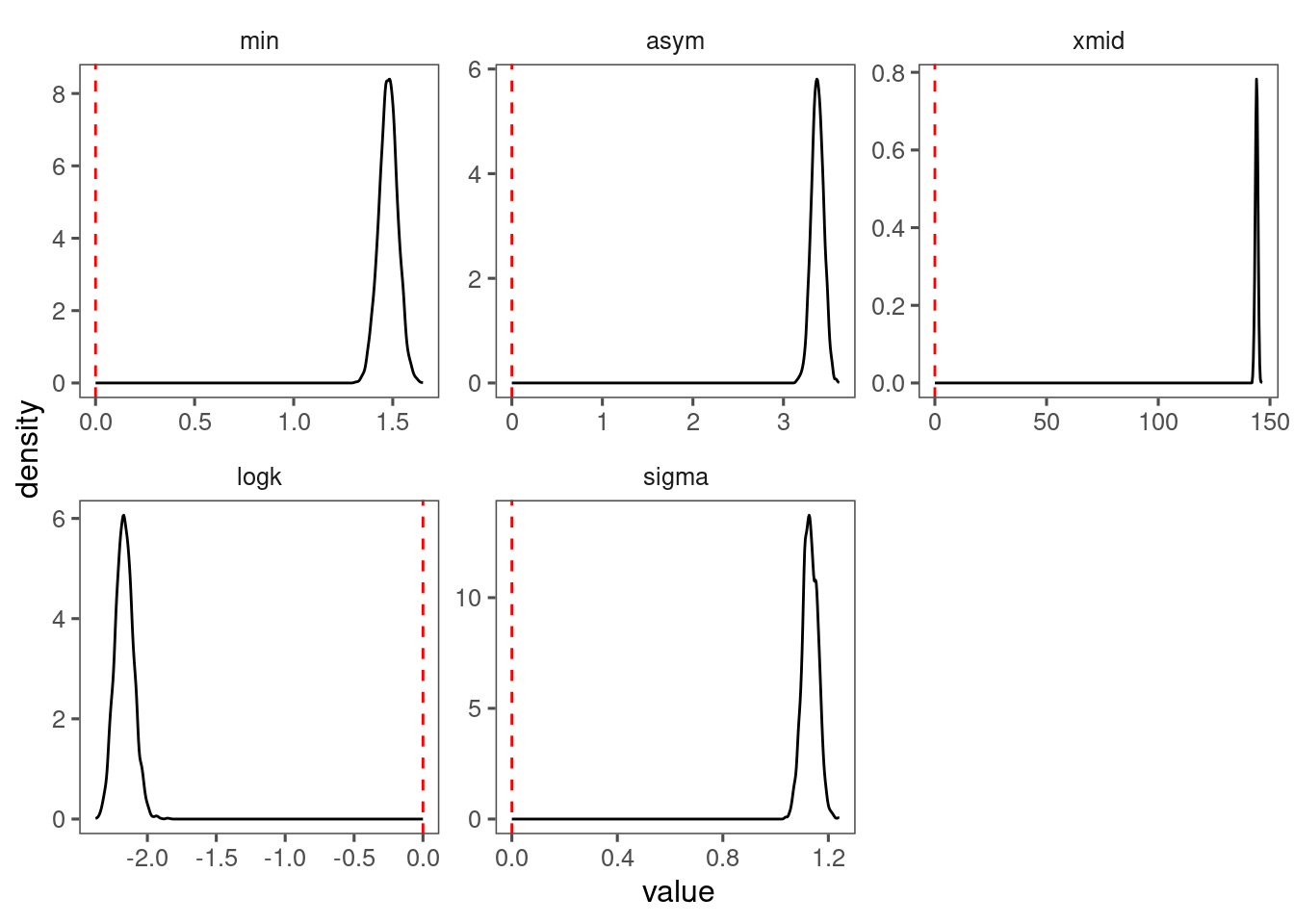
Make predictions
df_pred_1 <- calc_bayes_predict(
data = dat_1 %>%
distinct(doy),
df_MCMC = df_MCMC_1,
version = 1
)
write_rds(df_pred_1, "alldata/intermediate/shootmodeling/df_pred_1.rds")
df_pred_1 <- read_rds("alldata/intermediate/shootmodeling/df_pred_1.rds")
p_bayes_predict <- plot_bayes_predict(
data = dat_1,
data_predict = df_pred_1,
vis_log = T
)
p_bayes_predict$p_original
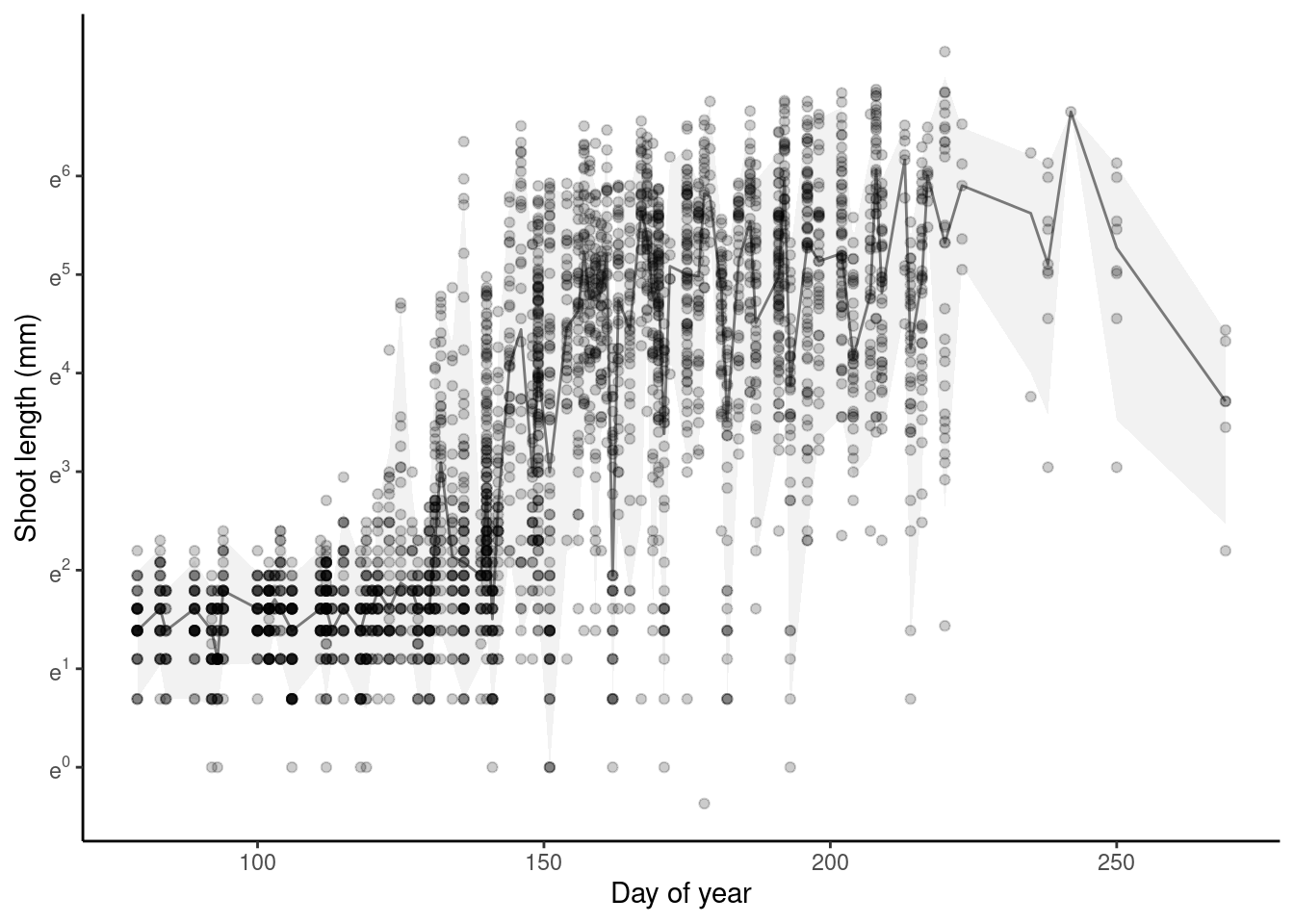
p_bayes_predict$p_overlay
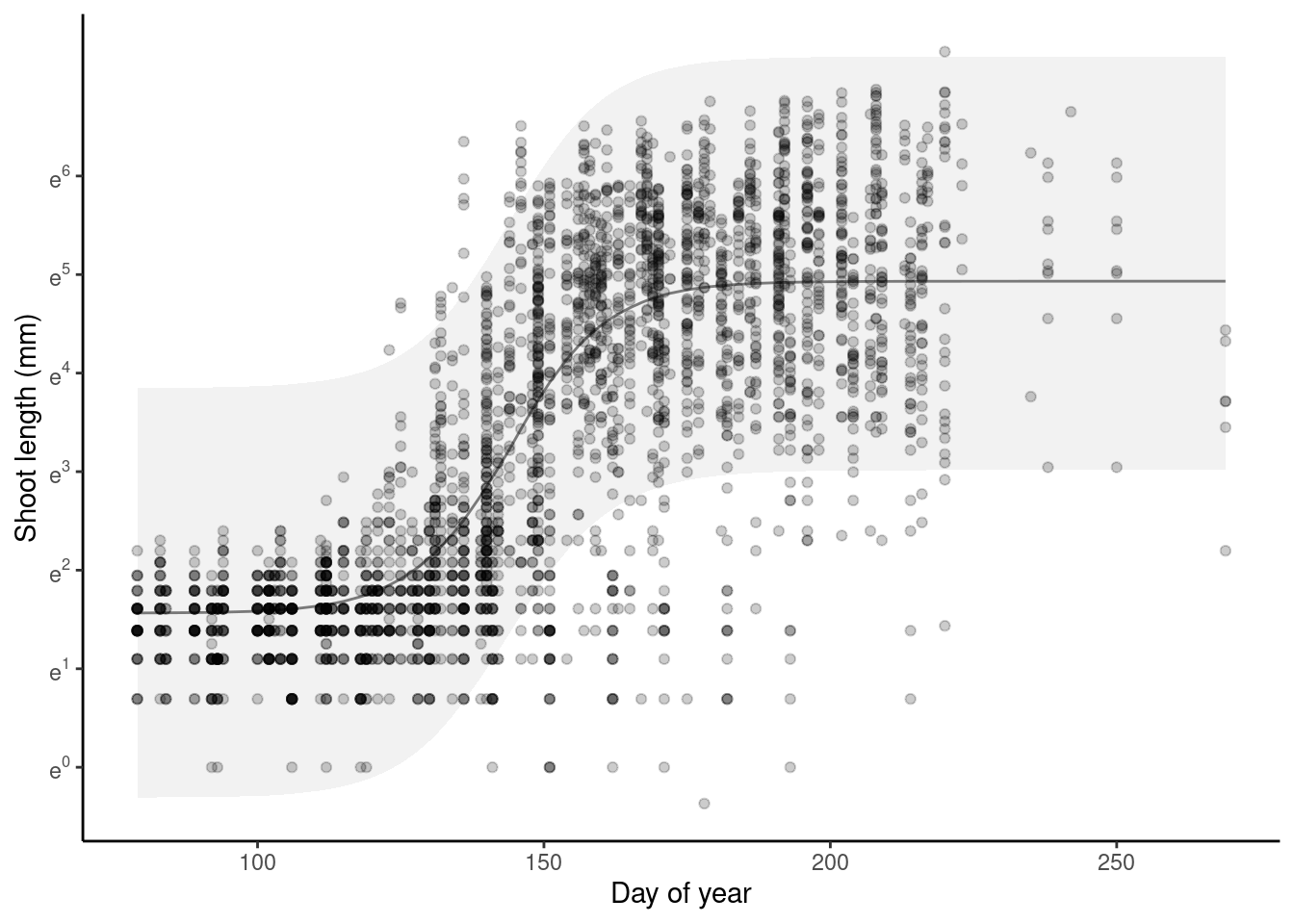
p_bayes_predict$p_accuracy
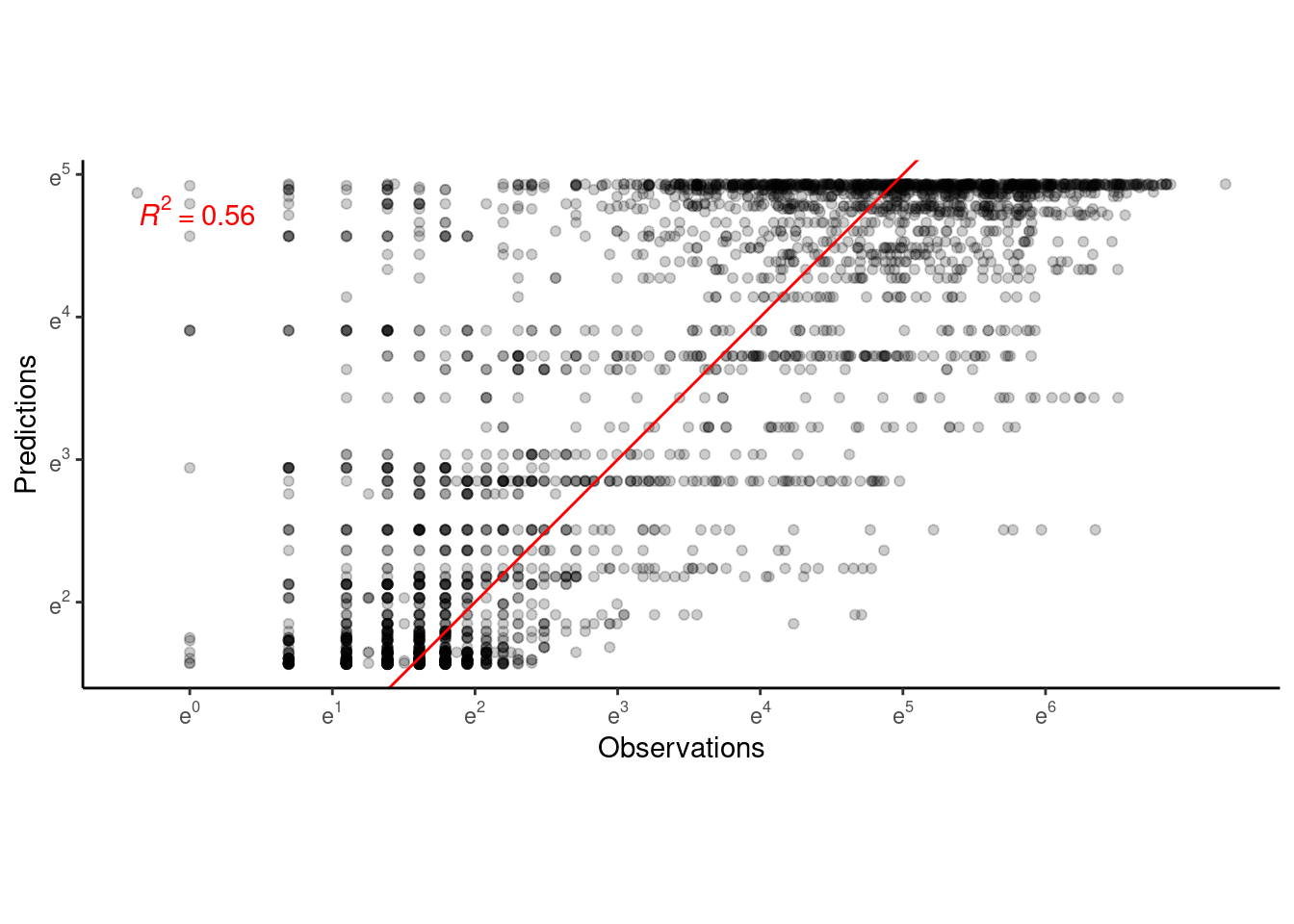
- Model captures the general trend of shoot growth.
- Think about the meaning of starting value of log-transformed shoot growth. Is it related to the precision of measurements? Why does shoot length start from positive values?
Bayesian model 2
Block-level random effects, no covariates.
Model
Data model
\begin{align*} y_{i^{(j)},j,t,d} \sim \text{Lognormal}(\mu_{j,d}, \sigma^2) \end{align*}
Process model
\begin{align*} \mu_{j,d} = c+\frac{A_j}{1+e^{-k_j(d-x_{0 j})}} \end{align*}
Random effects
\begin{align*} A_j &\sim \text{Normal}(\mu_A, \sigma_A^2) \newline x_{0 j} &\sim \text{Normal}(\mu_{x_0}, \sigma_{x_0}^2) \newline log(k_j) &\sim \text{Normal}(\mu_{log(k)}, \sigma_{log(k)}^2) \end{align*}
Priors
\begin{align*} c &\sim \text{Normal}(0, 1) \newline \mu_A &\sim \text{Normal}(5, 1) \newline \sigma_A^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \newline \mu_{x_0} &\sim \text{Normal}(160, 100) \newline \sigma_{x_0}^2 &\sim \text{Truncated Normal}(0, 100, 0, \infty) \newline \mu_{log(k)} &\sim \text{Normal}(-2, 0.04) \newline \sigma_{log(k)}^2 &\sim \text{Truncated Normal}(0, 0.04, 0, \infty) \newline \sigma^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \end{align*}
Prepare data
dat_2 <- dat_shoot_cov %>%
filter(species == "queru", canopy == "open", site == "cfc") %>%
filter(shoot > 0) %>%
mutate(group = block %>% factor() %>% as.integer())
Fit model
df_MCMC_2 <- calc_bayes_fit(
data = dat_2 %>% mutate(tag = "training"),
version = 2
)
write_rds(df_MCMC_2, "alldata/intermediate/shootmodeling/df_MCMC_2.rds")
df_MCMC_2 <- read_rds("alldata/intermediate/shootmodeling/df_MCMC_2.rds")
p_bayes_diagnostics <- plot_bayes_diagnostics(df_MCMC = df_MCMC_2)
p_bayes_diagnostics$p_MCMC
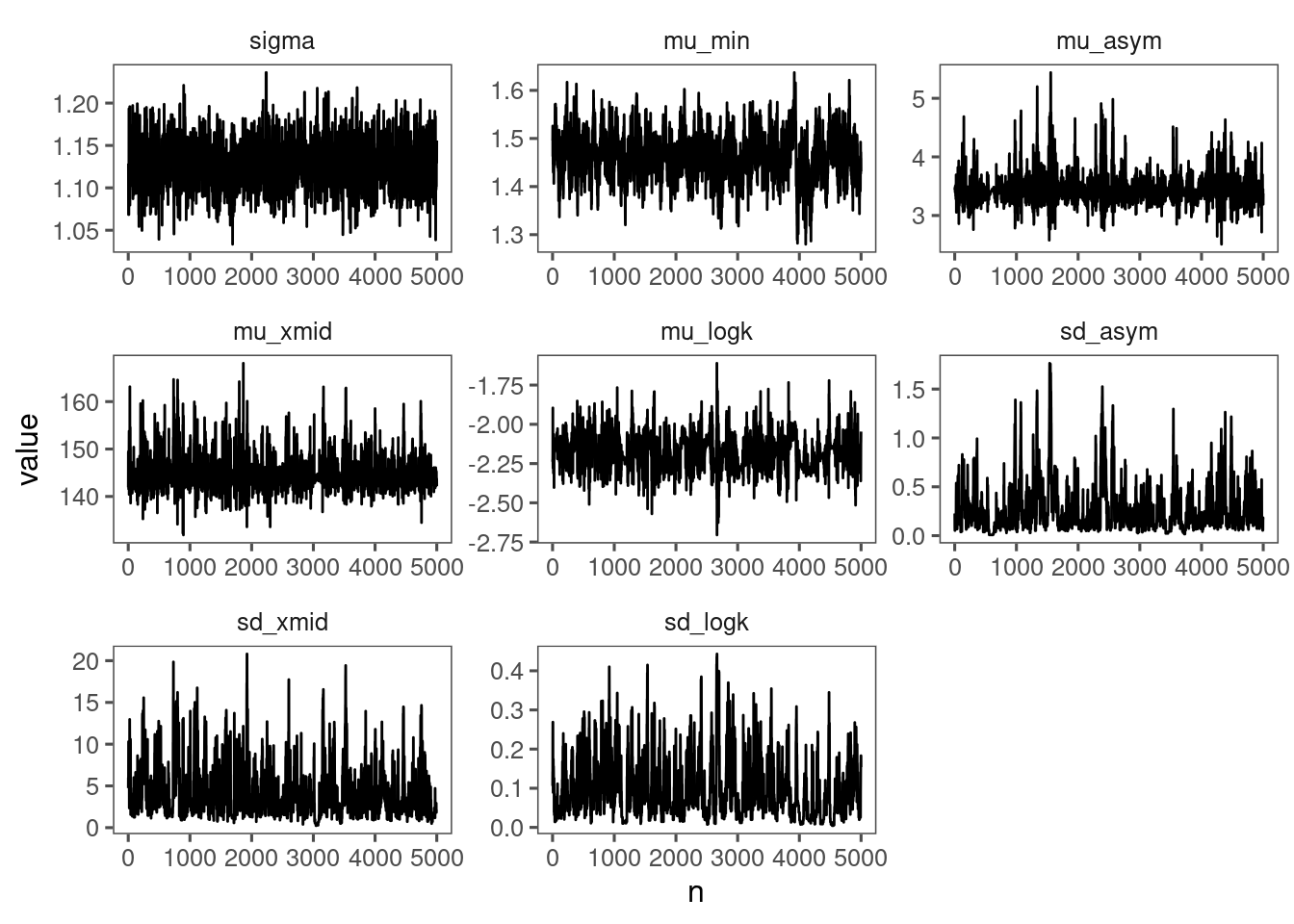
p_bayes_diagnostics$p_posterior
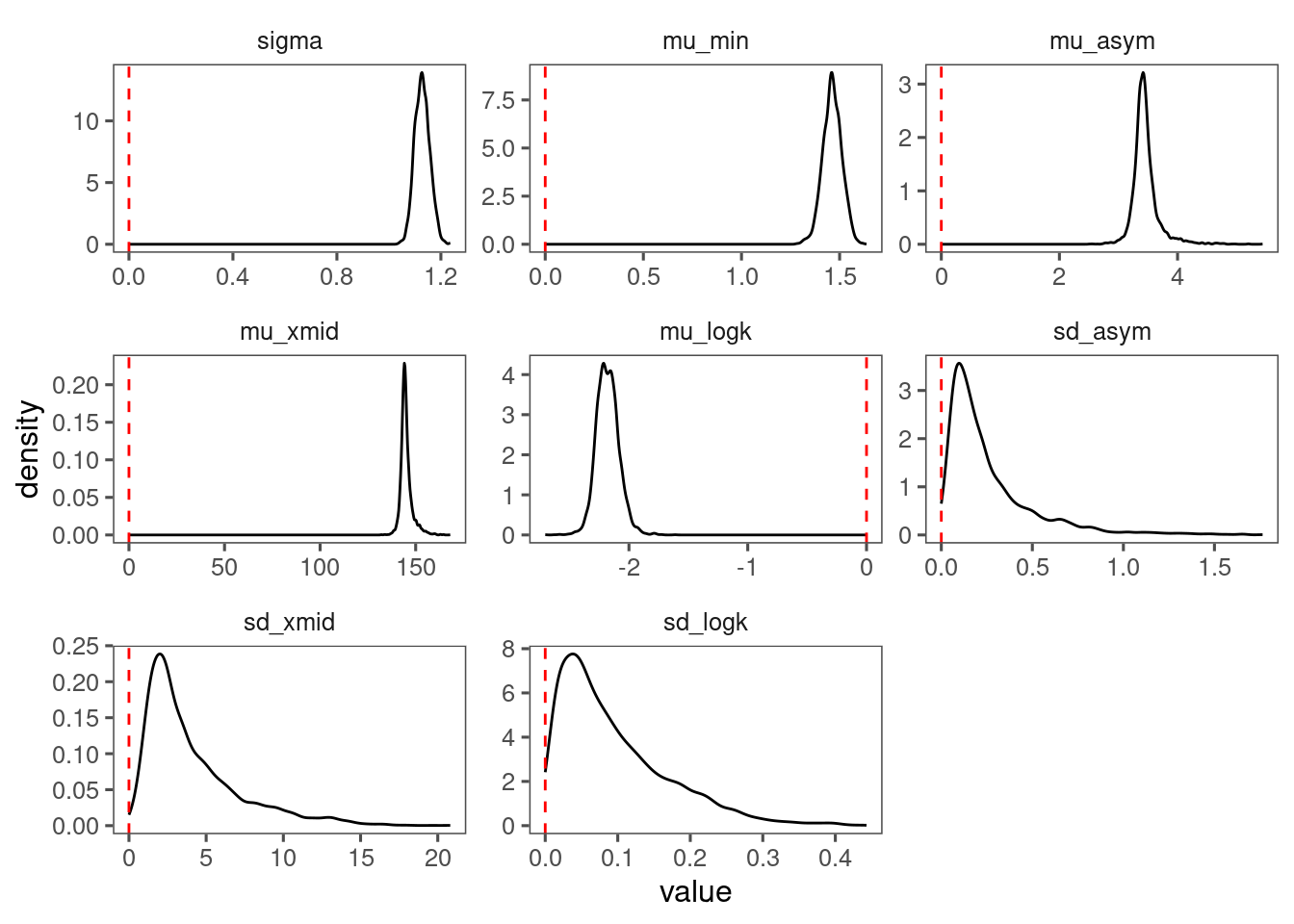
Make predictions
df_pred_2 <- calc_bayes_predict(
data = dat_2 %>%
distinct(group, doy),
df_MCMC = df_MCMC_2,
version = 2
)
write_rds(df_pred_2, "alldata/intermediate/shootmodeling/df_pred_2.rds")
df_pred_2 <- read_rds("alldata/intermediate/shootmodeling/df_pred_2.rds")
p_bayes_predict <- plot_bayes_predict(
data = dat_2,
data_predict = df_pred_2,
vis_log = T
)
p_bayes_predict$p_original
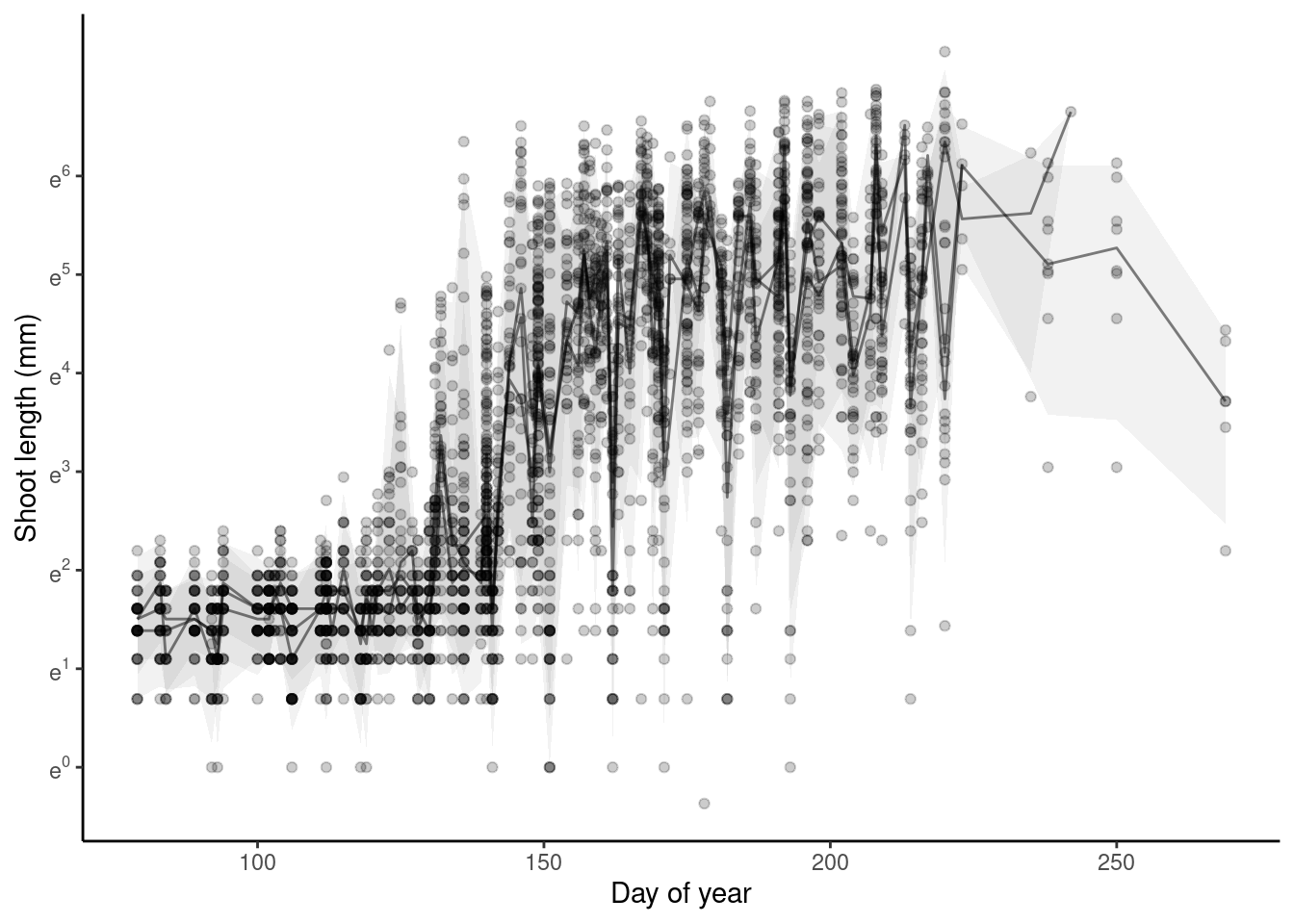
p_bayes_predict$p_overlay
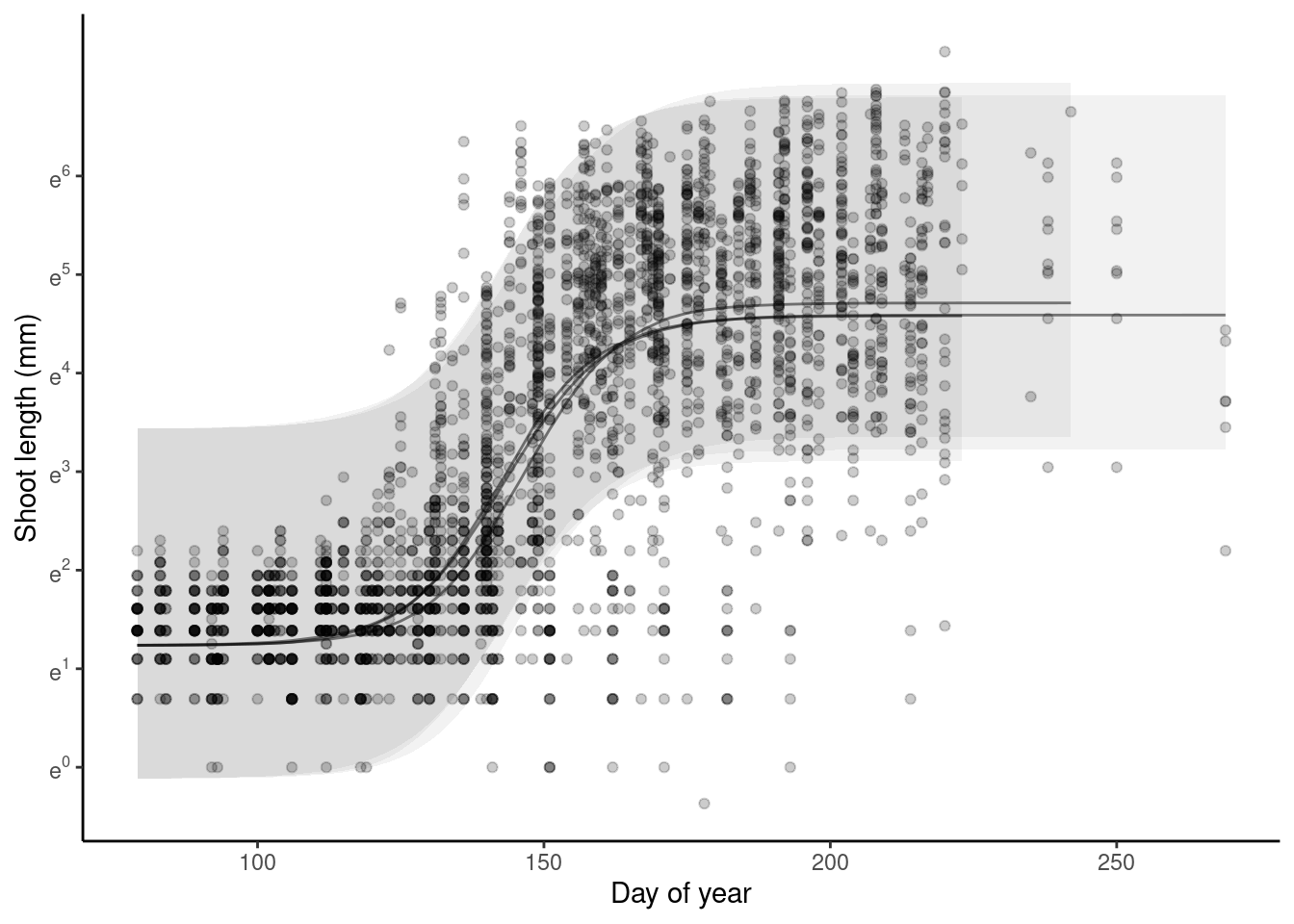
p_bayes_predict$p_accuracy
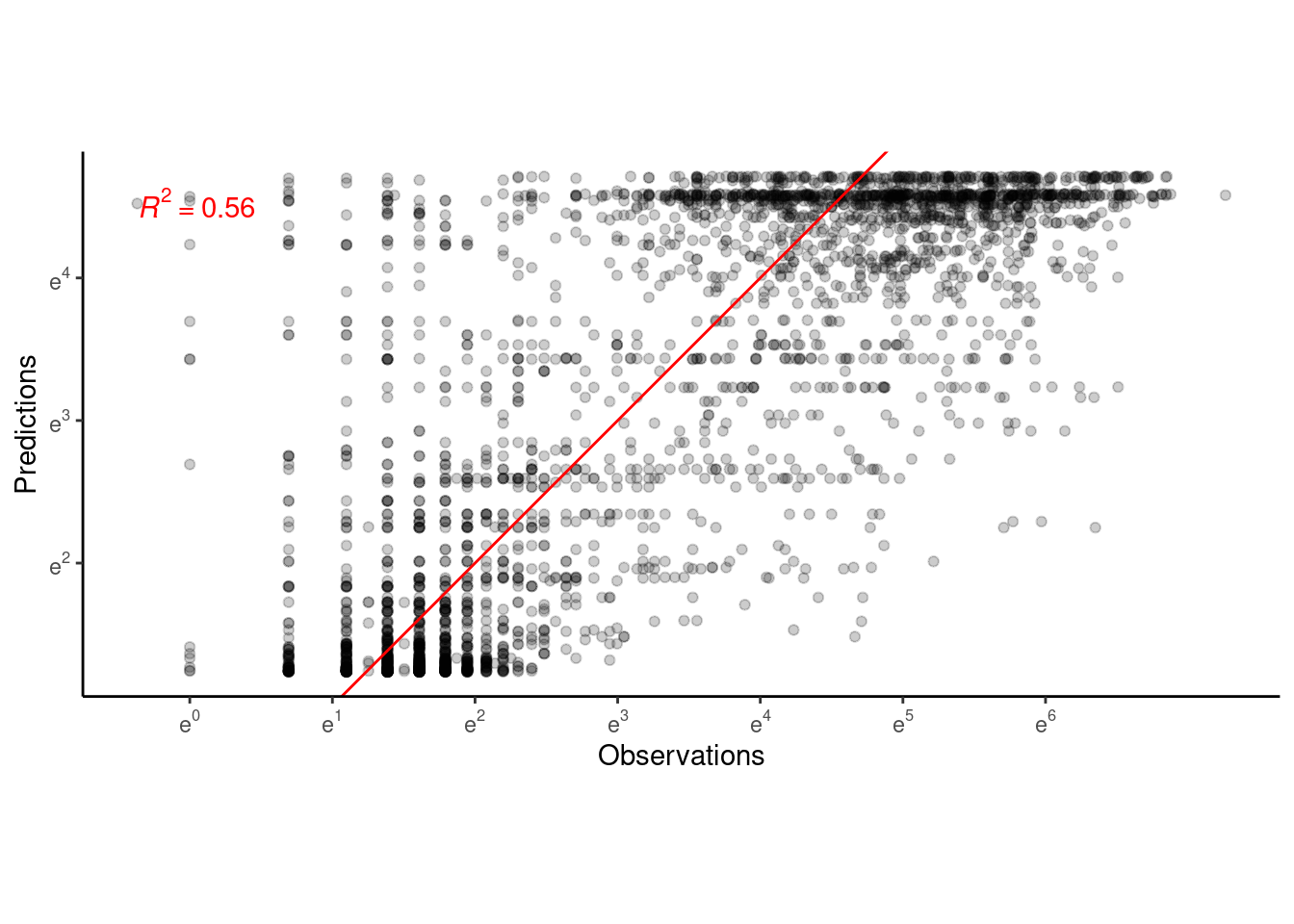
- Block-level random effects did not increase the amount of variability explained.
- Differences between blocks did not seem to be greater than differences between individuals and years.
- Do we still need block-level random effects?
- Note that the same structure can be used to implement individual-year-level random effects, although much slower. Individual-year-level random effects would be necessary if individuals and years are sampled very differently. What do you think?
Bayesian model 3
Block-level random effects, treatments as covariates.
Model
Data model
\begin{align*} y_{i^{(j)},j,t,d} \sim \text{Lognormal}(\mu_{i^{(j)},j,d}, \sigma^2) \end{align*}
Process model
\begin{align*} \mu_{i^{(j)},j,d} &= c+\frac{A_{i^{(j)},j}}{1+e^{-k_j(d-x_{0 i^{(j)},j})}} \newline A_{i^{(j)},j} &= \mu_A + \delta_{A,i^{(j)}}+ \alpha_{A,j} \newline x_{0 i^{(j)},j} &= \mu_{x_0} + \delta_{x_0,i^{(j)}}+ \alpha_{x_0,j} \newline log(k_{i^{(j)},j}) &= \mu_{log(k)} + \delta_{log(k),i^{(j)}}+ \alpha_{log(k),j} \newline \end{align*}
Fixed effects
\begin{align*} \delta_{A,i^{(j)}} &= \beta_{A,1} T_{i^{(j)}} + \beta_{A,2} D_{i^{(j)}} + \beta_{A,3} T_{i^{(j)}} D_{i^{(j)}} \newline \delta_{x_0,i^{(j)}} &= \beta_{x_0,1} T_{i^{(j)}} + \beta_{x_0,2} D_{i^{(j)}} + \beta_{x_0,3} T_{i^{(j)}} D_{i^{(j)}} \newline \delta_{log(k),i^{(j)}} &= \beta_{log(k),1} T_{i^{(j)}} + \beta_{log(k),2} D_{i^{(j)}} + \beta_{log(k),3} T_{i^{(j)}} D_{i^{(j)}} \end{align*}
Random effects
\begin{align*} \alpha_{A,j} &\sim \text{Normal}(0, \sigma_A^2) \newline \alpha_{x_0,j} &\sim \text{Normal}(0, \sigma_{x_0}^2) \newline \alpha_{log(k),j} &\sim \text{Normal}(0, \sigma_{log(k)}^2) \end{align*}
Priors
\begin{align*} c &\sim \text{Normal}(0, 1) \newline \mu_A &\sim \text{Normal}(5, 1) \newline \beta_A &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 1 & 0 & 0 \newline 0 & 1 & 0 \newline 0 & 0 & 1 \newline \end{pmatrix} )\newline \sigma_A^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \newline \mu_{x_0} &\sim \text{Normal}(160, 100) \newline \beta_{x_0} &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 100 & 0 & 0 \newline 0 & 100 & 0 \newline 0 & 0 & 100 \newline \end{pmatrix} )\newline \sigma_{x_0}^2 &\sim \text{Truncated Normal}(0, 100, 0, \infty) \newline \mu_{log(k)} &\sim \text{Normal}(-2, 0.04) \newline \beta_{log(k)} &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 0.04 & 0 & 0 \newline 0 & 0.04 & 0 \newline 0 & 0 & 0.04 \newline \end{pmatrix} )\newline \sigma_{log(k)}^2 &\sim \text{Truncated Normal}(0, 0.04, 0, \infty) \newline \sigma^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \end{align*}
Prepare data
dat_3 <- dat_shoot_cov %>%
filter(species == "queru", canopy == "open", site == "cfc") %>%
filter(shoot > 0) %>%
mutate(group = block %>% factor() %>% as.integer()) %>%
mutate(heat_trt = factor(heat_name, levels = c("ambient", "+1.7C", "+3.4C"), labels = c(0, 1, 2)) %>% as.character() %>% as.integer()) %>%
mutate(water_trt = factor(water_name, levels = c("ambient", "reduced"), labels = c(0, 1)) %>% as.character() %>% as.integer())
Fit model
df_MCMC_3 <- calc_bayes_fit(
data = dat_3 %>% mutate(tag = "training"),
version = 3
)
write_rds(df_MCMC_3, "alldata/intermediate/shootmodeling/df_MCMC_3.rds")
df_MCMC_3 <- read_rds("alldata/intermediate/shootmodeling/df_MCMC_3.rds") %>% tidy_mcmc(dat_3)
p_bayes_diagnostics <- plot_bayes_diagnostics(df_MCMC = df_MCMC_3)
p_bayes_diagnostics$p_MCMC
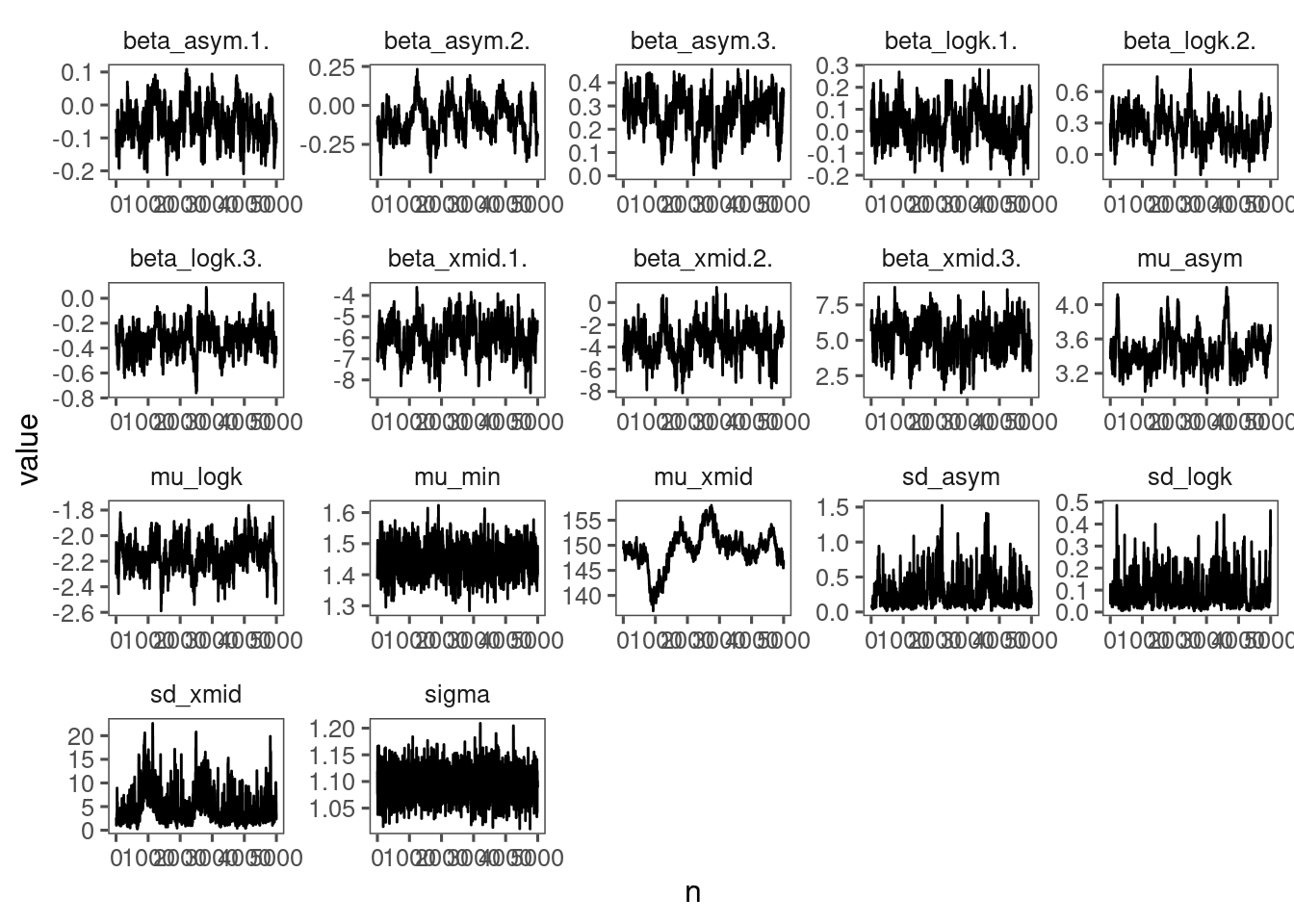
p_bayes_diagnostics$p_posterior
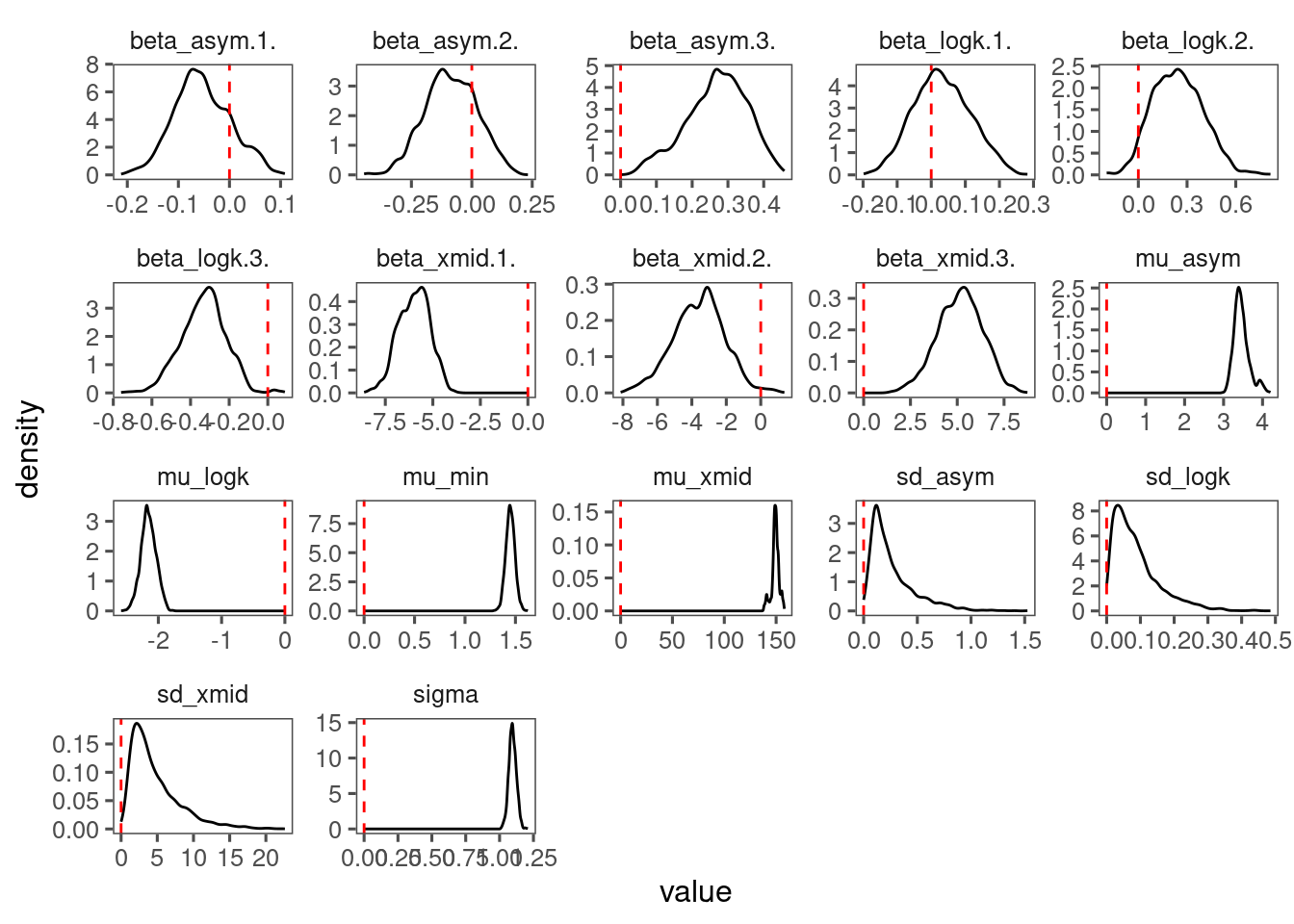
p_bayes_diagnostics$p_coefficient
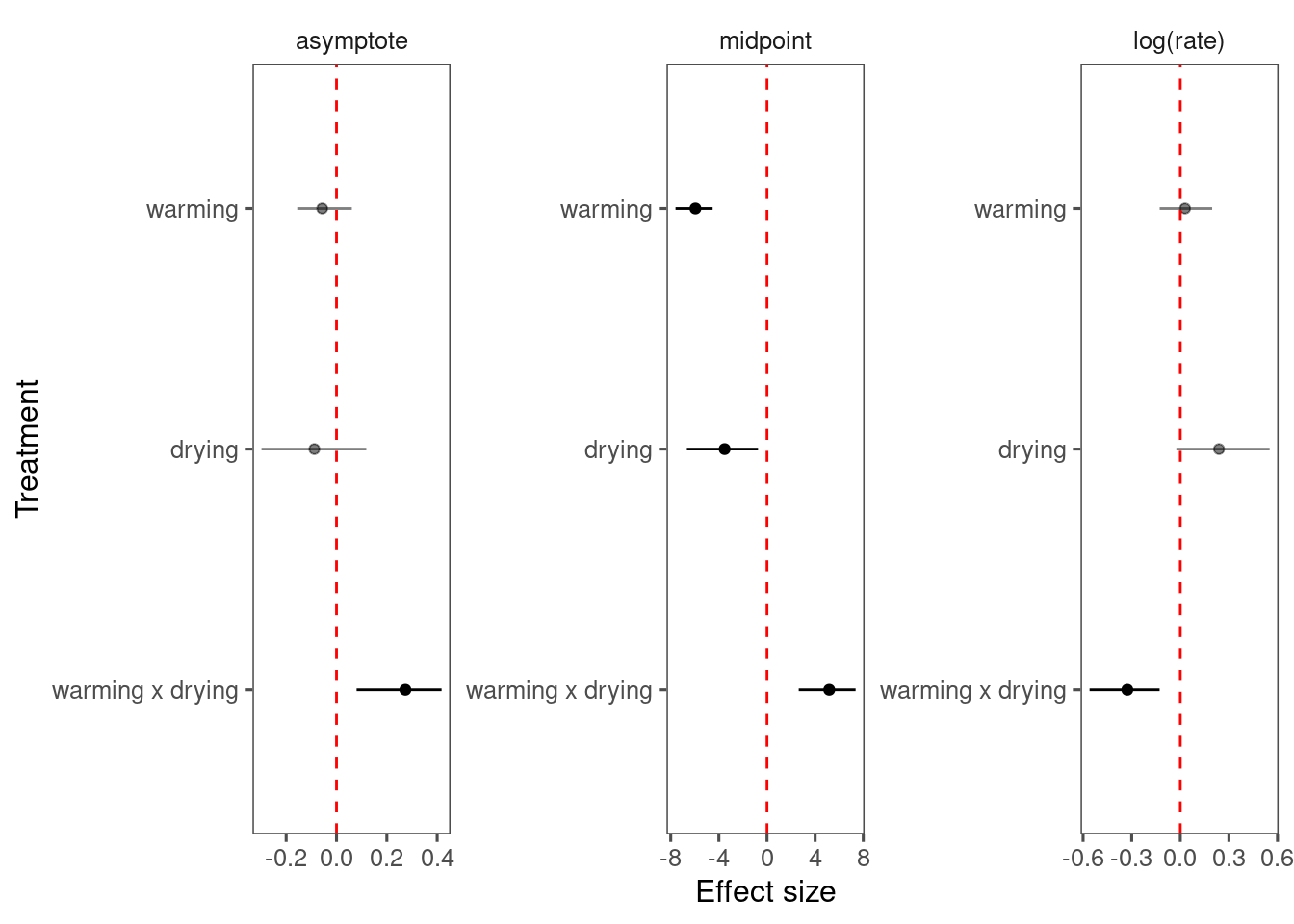
Make predictions
df_pred_3 <- calc_bayes_predict(
data = dat_3 %>%
distinct(group, heat_trt, water_trt, doy),
df_MCMC = df_MCMC_3,
version = 3
)
write_rds(df_pred_3, "alldata/intermediate/shootmodeling/df_pred_3.rds")
df_pred_3 <- read_rds("alldata/intermediate/shootmodeling/df_pred_3.rds")
p_bayes_predict <- plot_bayes_predict(
data = dat_3,
data_predict = df_pred_3,
vis_log = T
)
p_bayes_predict$p_original
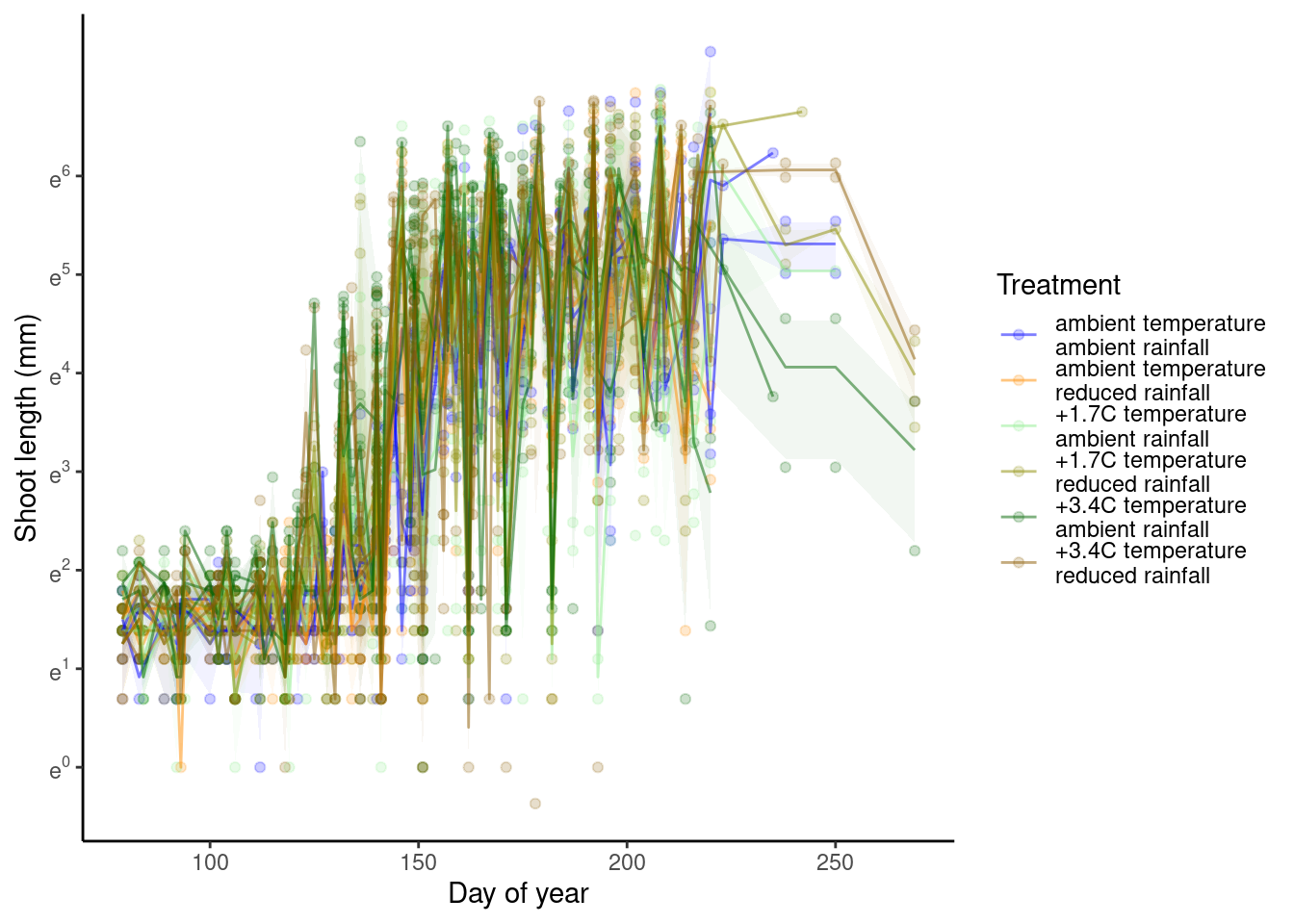
p_bayes_predict$p_overlay
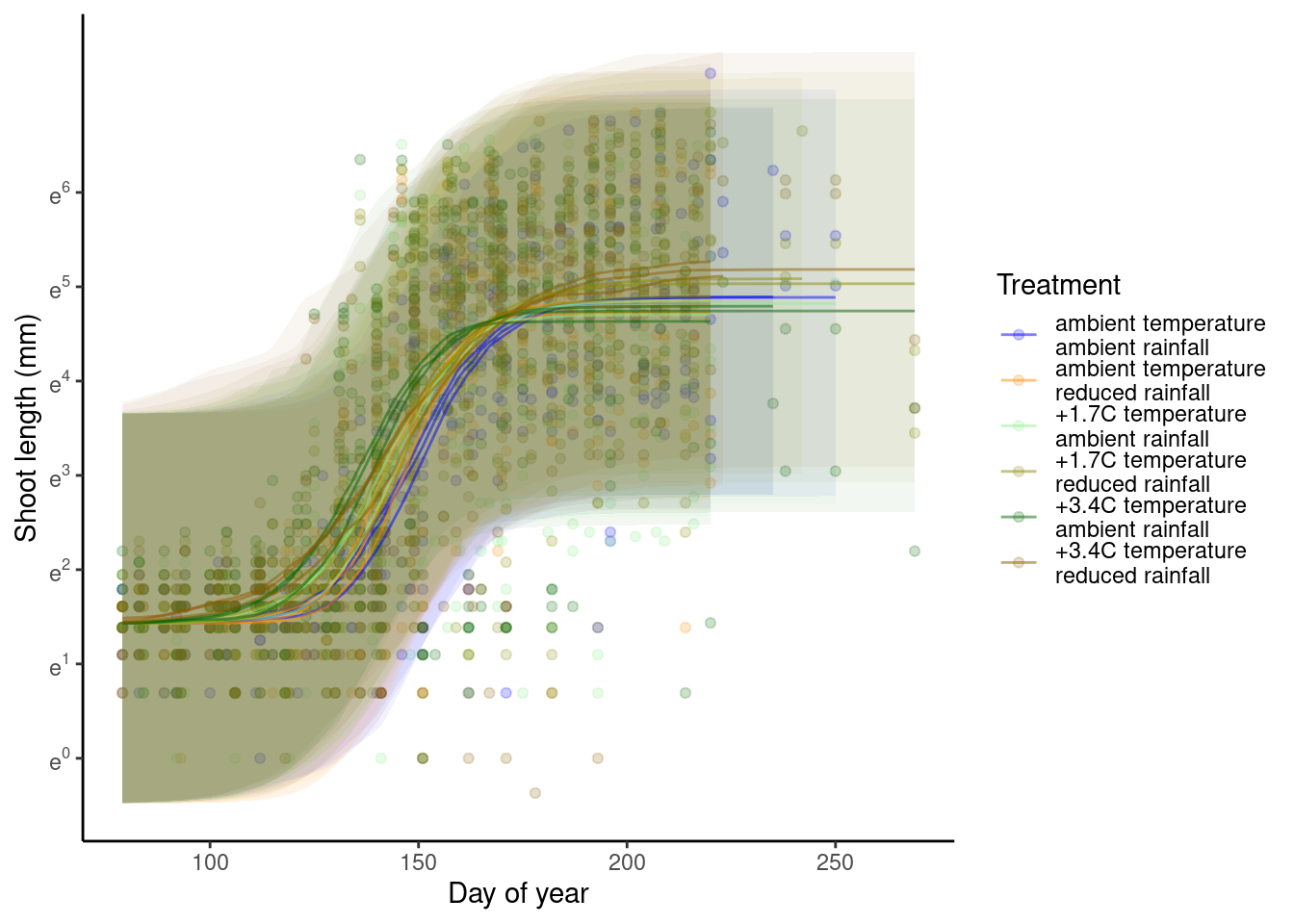
p_bayes_predict$p_accuracy

- Warming advances shoot growth.
- Rainfall reduces also advances shoot growth when applied alone.
- Rainfall reduction offsets the advancing effects of warming.
- No clear treatment effects on asymptote, probably because asympote is more determined by variability between individuals and years.
- Covariates did not really increase the amount of variability explained, probably because of large variability between individuals and years in starting values and asymptotes.
- Again, block-level random effects seems to make little difference.
Bayesian model 4
Shoot-year-level random effects, treatments as covariates.
Model
Data model
\begin{align*} y_{i,t,d} \sim \text{Lognormal}(\mu_{i,t,d}, \sigma^2) \end{align*}
Process model
\begin{align*} \mu_{i,t,d} &= c+\frac{A_{i,t}}{1+e^{-k_{i,t}(d-x_{0 i,t})}} \newline A_{i,t} &= \mu_A + \delta_{A,i}+ \alpha_{A,i,t} \newline x_{0 i,t} &= \mu_{x_0} + \delta_{x_0,i}+ \alpha_{x_0,i,t} \newline log(k_{i,t}) &= \mu_{log(k)} + \delta_{log(k),i}+ \alpha_{log(k),i,t} \end{align*}
Fixed effects
\begin{align*} \delta_{A,i} &= \beta_{A,1} T_i + \beta_{A,2} D_i + \beta_{A,3} T_i D_i \newline \delta_{x_0,i} &= \beta_{x_0,1} T_i + \beta_{x_0,2} D_i + \beta_{x_0,3} T_i D_i \newline \delta_{log(k),i} &= \beta_{log(k),1} T_i + \beta_{log(k),2} D_i + \beta_{log(k),3} T_i D_i \end{align*}
Random effects
\begin{align*} \alpha_{A,i,t} &\sim \text{Normal}(0, \sigma_A^2) \newline \alpha_{x_0,i,t} &\sim \text{Normal}(0, \sigma_{x_0}^2) \newline \alpha_{log(k),i,t} &\sim \text{Normal}(0, \sigma_{log(k)}^2) \end{align*}
Priors
\begin{align*} c &\sim \text{Normal}(0, 1) \newline \mu_A &\sim \text{Normal}(5, 1) \newline \beta_A &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 1 & 0 & 0 \newline 0 & 1 & 0 \newline 0 & 0 & 1 \newline \end{pmatrix} )\newline \sigma_A^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \newline \mu_{x_0} &\sim \text{Normal}(160, 100) \newline \beta_{x_0} &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 100 & 0 & 0 \newline 0 & 100 & 0 \newline 0 & 0 & 100 \newline \end{pmatrix} )\newline \sigma_{x_0}^2 &\sim \text{Truncated Normal}(0, 100, 0, \infty) \newline \mu_{log(k)} &\sim \text{Normal}(-2, 0.04) \newline \beta_{log(k)} &\sim \text{Multivariate Normal} ( \begin{pmatrix} 0 \newline 0 \newline 0 \newline \end{pmatrix}, \begin{pmatrix} 0.04 & 0 & 0 \newline 0 & 0.04 & 0 \newline 0 & 0 & 0.04 \newline \end{pmatrix} )\newline \sigma_{log(k)}^2 &\sim \text{Truncated Normal}(0, 0.04, 0, \infty) \newline \sigma^2 &\sim \text{Truncated Normal}(0, 1, 0, \infty) \end{align*}
Prepare data
dat_4 <- dat_shoot_cov %>%
filter(species == "queru", canopy == "open", site == "cfc") %>%
filter(shoot > 0) %>%
drop_na(barcode) %>%
mutate(slot = if_else(is.na(slot), "", slot)) %>%
mutate(group = str_c(barcode, slot, year, sep = "_") %>% factor() %>% as.integer()) %>%
mutate(heat_trt = factor(heat_name, levels = c("ambient", "+1.7C", "+3.4C"), labels = c(0, 1, 2)) %>% as.character() %>% as.integer()) %>%
mutate(water_trt = factor(water_name, levels = c("ambient", "reduced"), labels = c(0, 1)) %>% as.character() %>% as.integer())
Fit model
df_MCMC_4 <- calc_bayes_fit(
data = dat_4 %>% mutate(tag = "training"),
version = 4
)
write_rds(df_MCMC_4, "alldata/intermediate/shootmodeling/df_MCMC_4.rds")
df_MCMC_4 <- read_rds("alldata/intermediate/shootmodeling/df_MCMC_4.rds") %>% tidy_mcmc(dat_4)
p_bayes_diagnostics <- plot_bayes_diagnostics(df_MCMC = df_MCMC_4)
p_bayes_diagnostics$p_MCMC
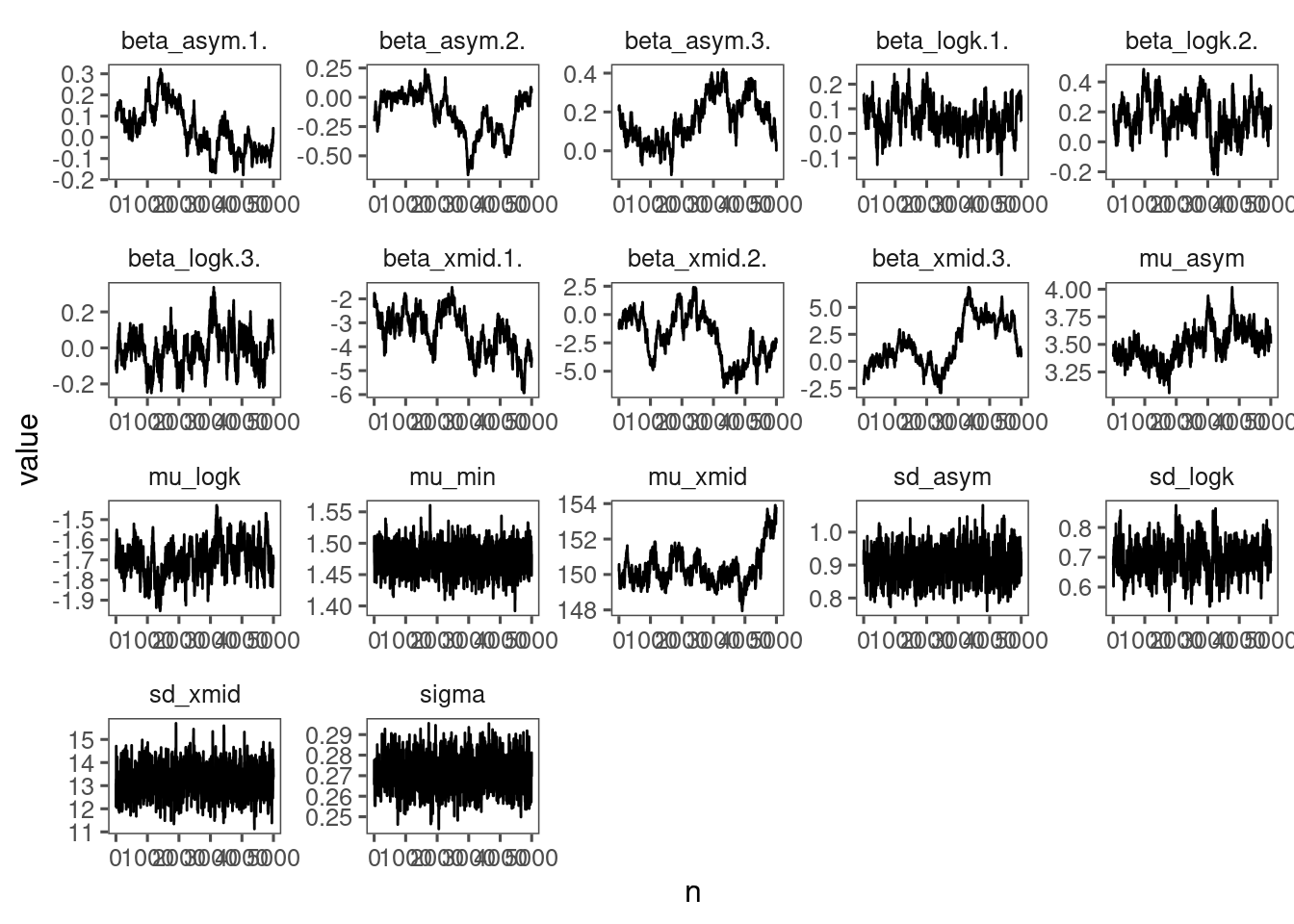
p_bayes_diagnostics$p_posterior
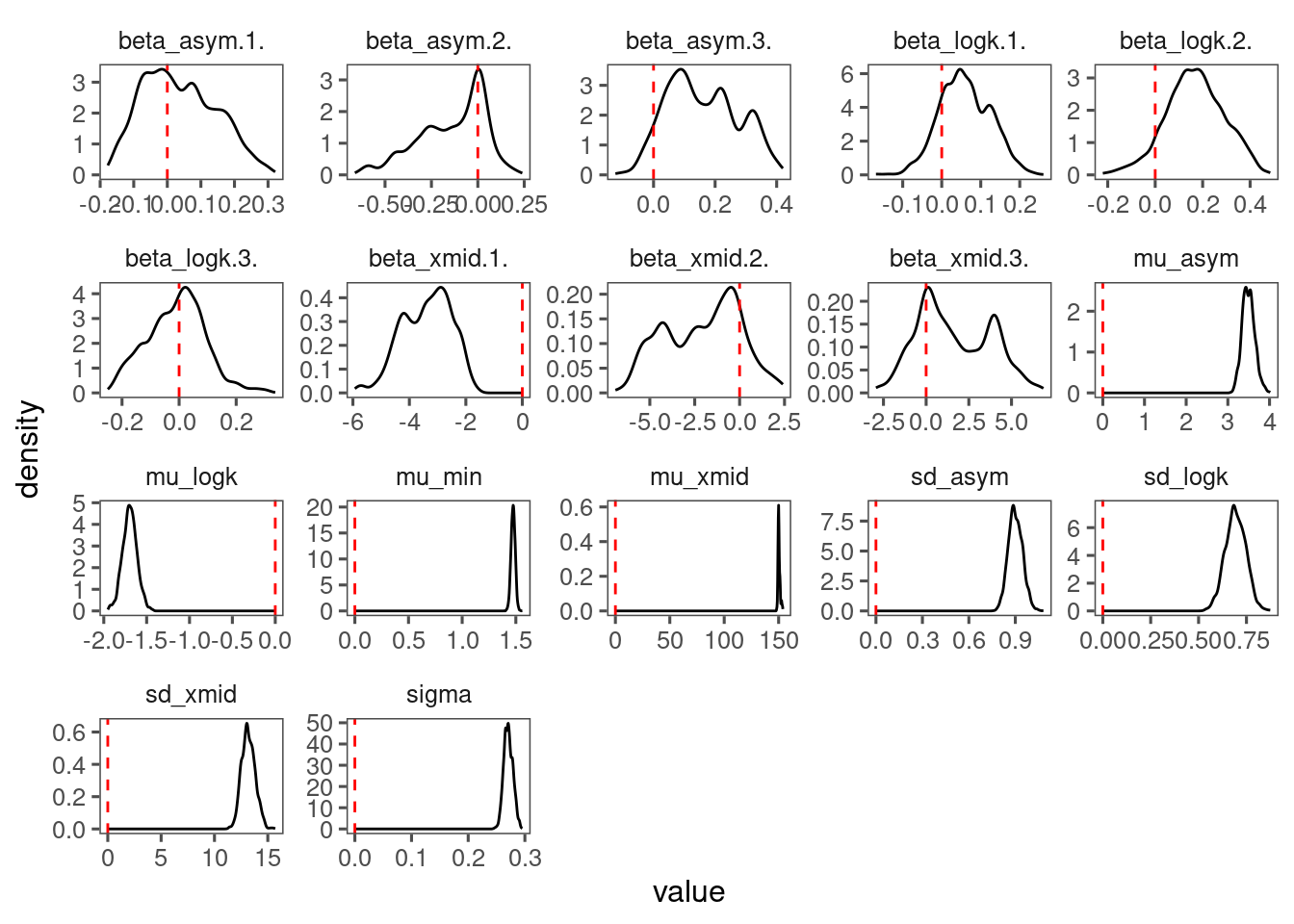
p_bayes_diagnostics$p_coefficient
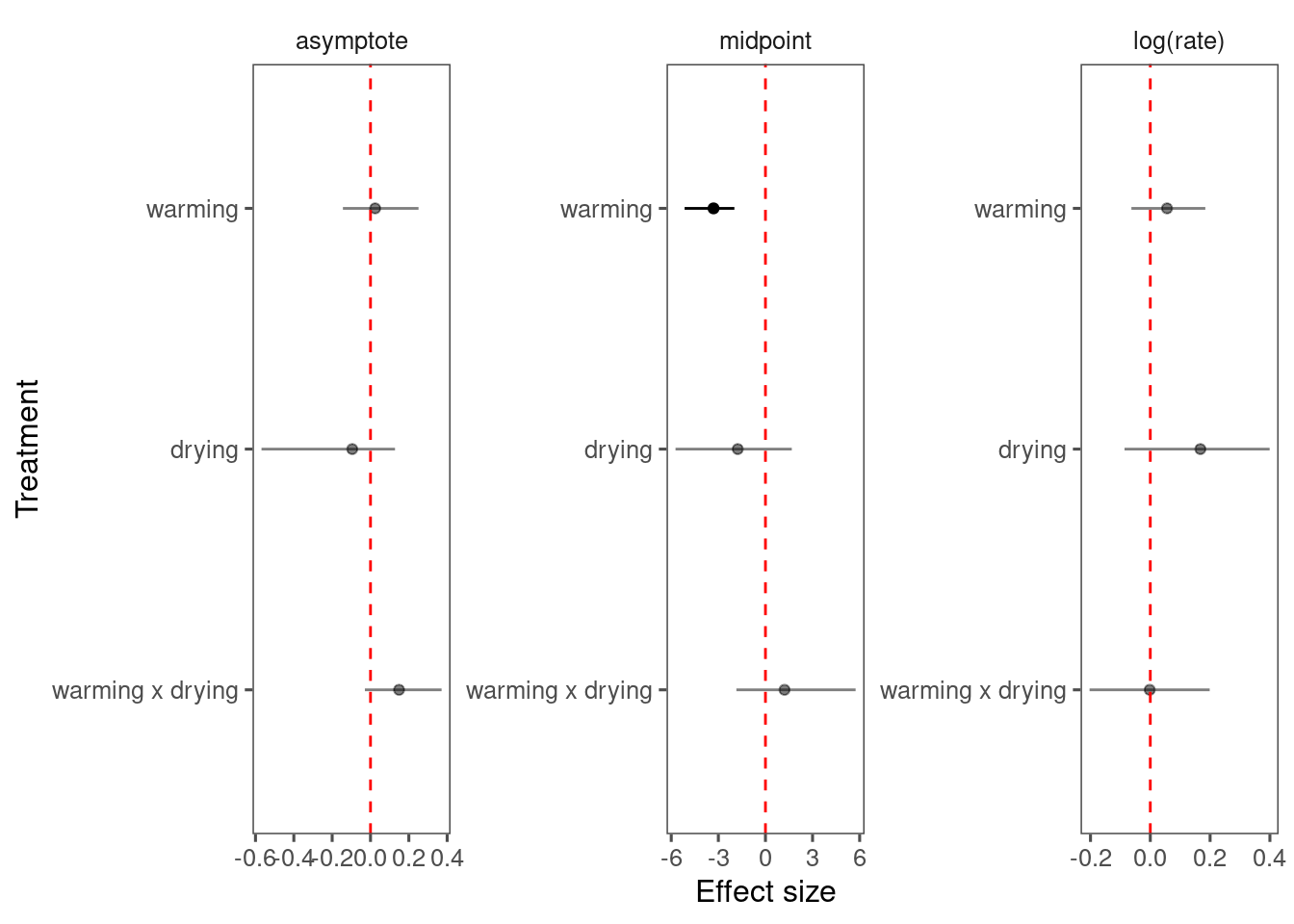
Make predictions
df_pred_4 <- calc_bayes_predict(
data = dat_4 %>%
distinct(group, heat_trt, water_trt, doy),
df_MCMC = df_MCMC_4,
version = 4
)
write_rds(df_pred_4, "alldata/intermediate/shootmodeling/df_pred_4.rds")
df_pred_4 <- read_rds("alldata/intermediate/shootmodeling/df_pred_4.rds")
p_bayes_predict <- plot_bayes_predict(
data = dat_4,
data_predict = df_pred_4,
vis_log = T
)
p_bayes_predict$p_original
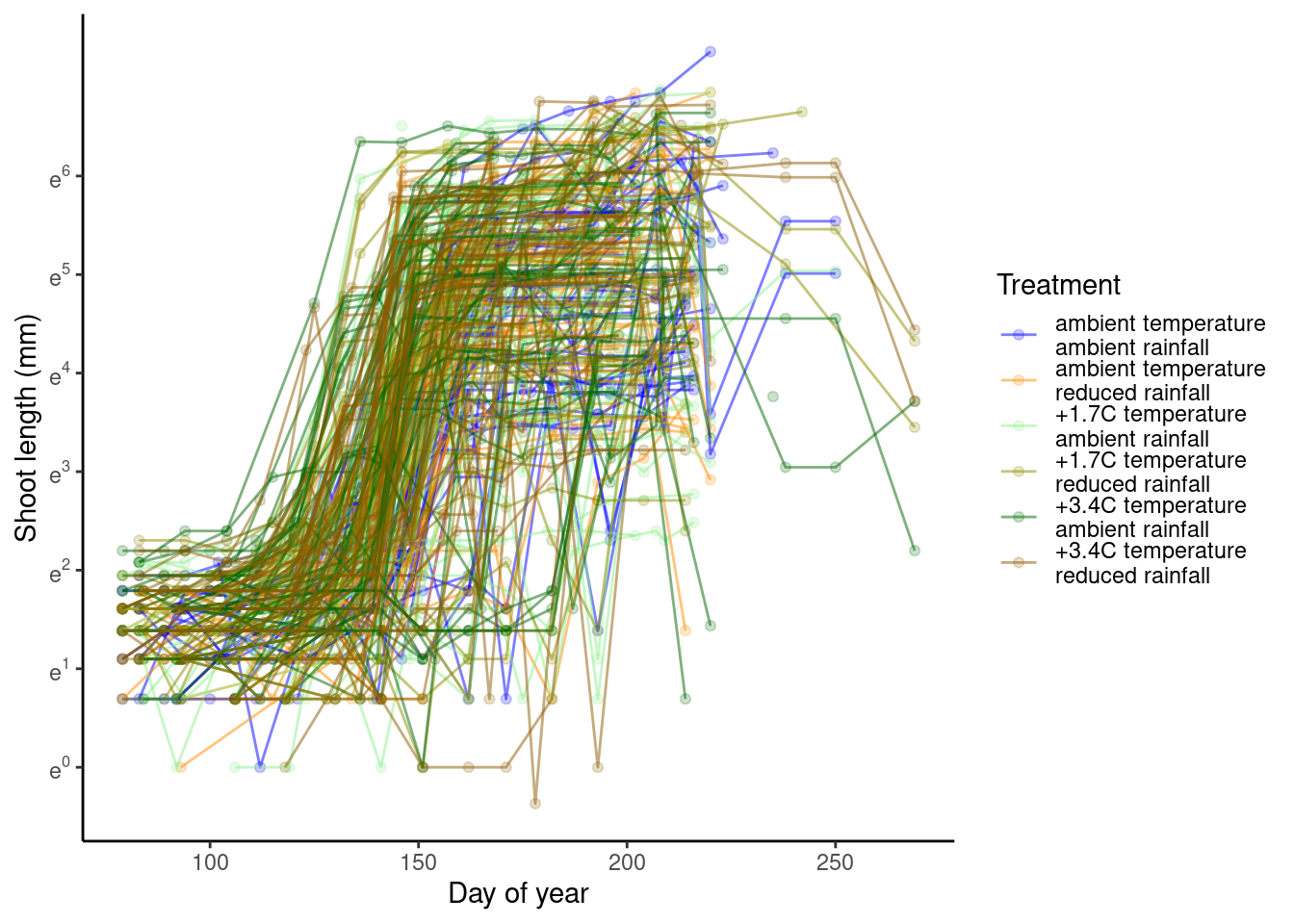
p_bayes_predict$p_overlay
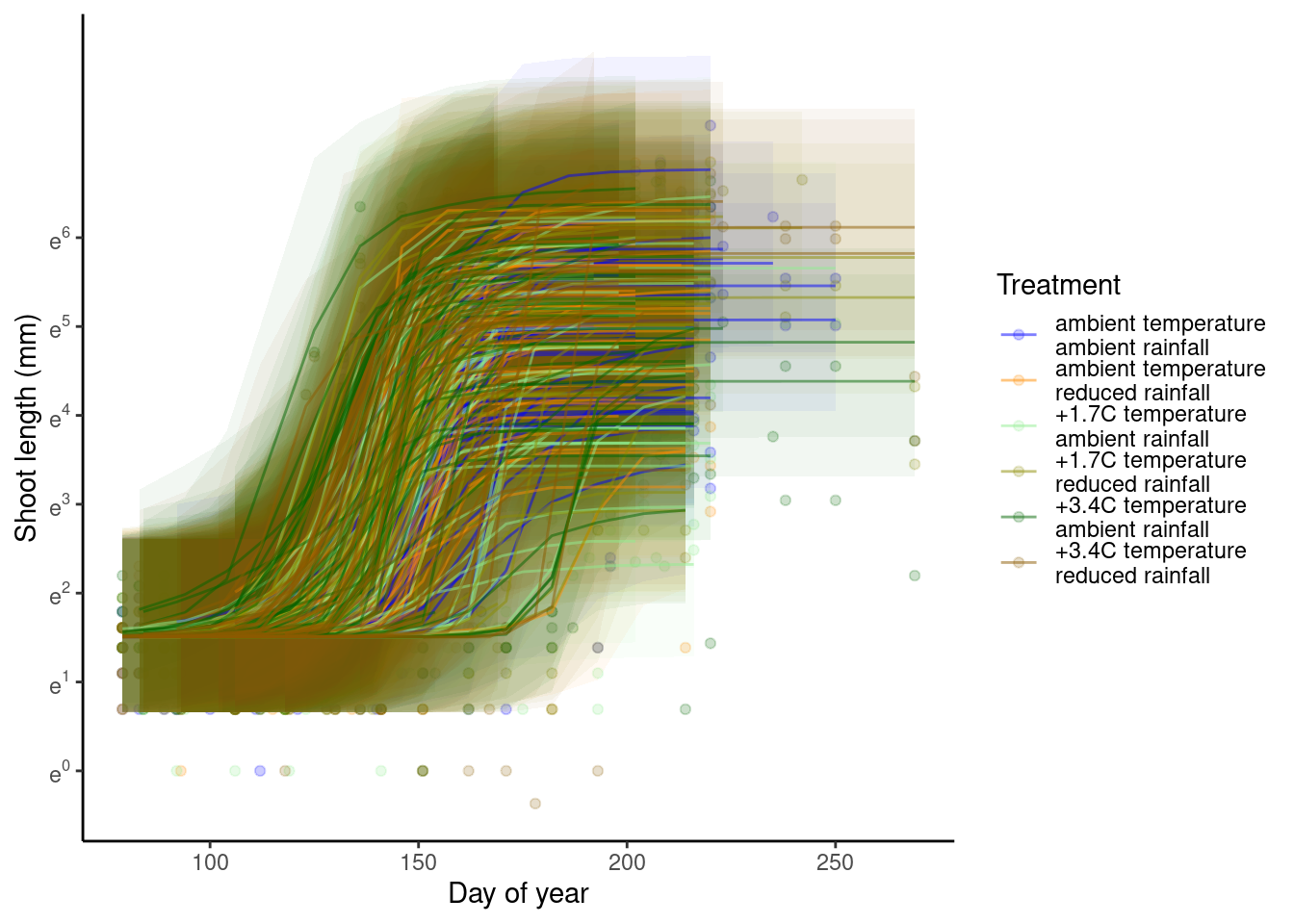
p_bayes_predict$p_accuracy
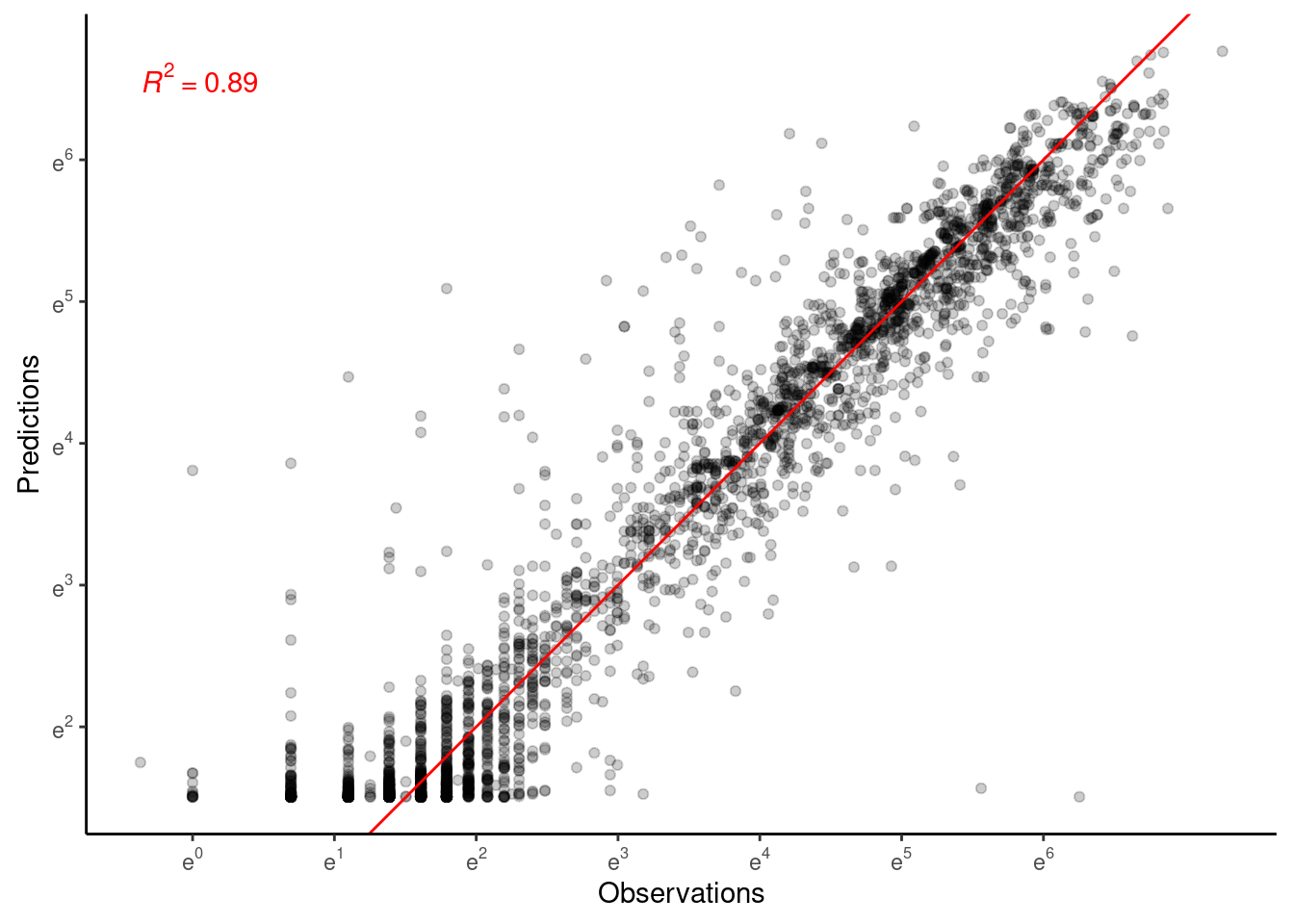
- Mixing is poor. Will need longer chains or simplified model structure.
- Perhaps remove covariates for asymptote?
- Treatment effects still clear.
- Model fit is greatly improved by shoot-year-level random effects.