Prepare ordinal data
Read in data from 2009 to 2020 in long format. Calculate time of first yes.
dat_phenophase_time <- calc_phenophase_time(dat_phenophase)
Convert binary (yes or no) data to ordinal (developmental stage) data. In this dataset, some individuals are scored as “budbreak” and “oneleaf” at the same time. I took the later stage. Note that I don’t have a category of “dormancy” because it can mean multiple things when scores for “budbreak” “oneleaf” and “mostleaf” are all zero.
dat_phenophase_ordinal <- tidy_phenophase_ordinal(dat_phenophase_time = dat_phenophase_time, season = "spring", keepfirst = T)
Table: Table 1: Examples of ordinal stage determination.
| budbreak | oneleaf | mostleaf | stage |
|---|---|---|---|
| 1 | 0 | 0 | budbreak |
| 0 | 1 | 0 | oneleaf |
| 0 | 0 | 1 | mostleaf |
| 0 | 1 | 1 | mostleaf |
| 1 | 1 | 0 | oneleaf |
| 1 | 1 | 1 | mostleaf |
plot_phenophase_ordinal(dat_phenophase_ordinal)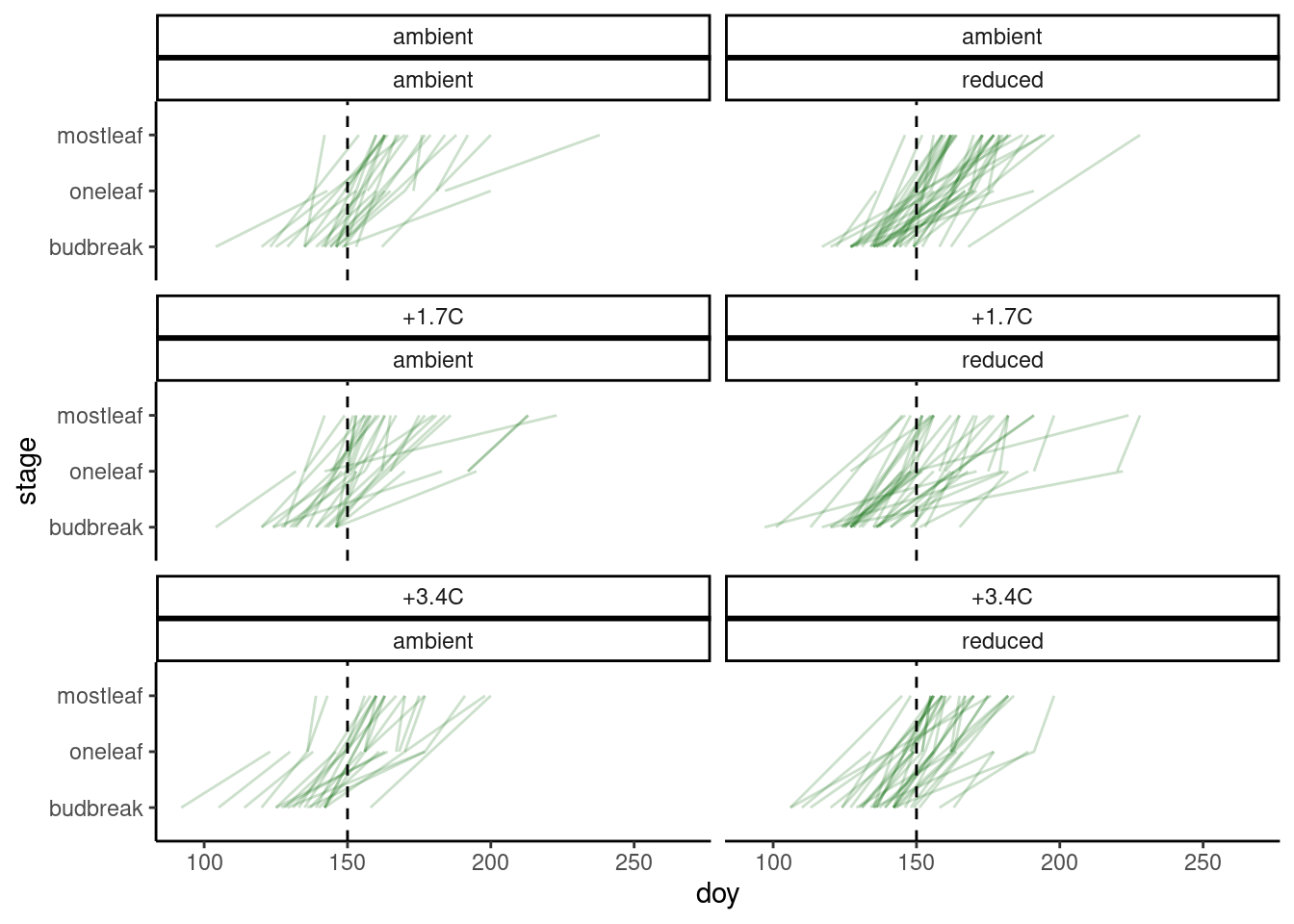
Figure 1: Changes in developmental stage over time of randomly selected individuals.
Ordinal regression
My simplest model:
$$ logit(P(S_i \le j))= \theta_j - \beta X_i $$
$$ X = [DOY, Heat+, Water-, Heat+ \times Water-, Heat+ \times DOY, Water- \times DOY] $$
$$ i = 1, …, n $$
$$ j = budbreak, oneleaf, mostleaf $$
This is a model for the cumulative probability of the ith stage observation falling in the jth category or below, where i index all observations, j index the response categories, and \theta_j is the intercept or threshold for the jth cumulative logit: logit(P(S_i <= j)).
I fit the model with the R package ordinal reference.
test_ordinal(dat_phenophase_ordinal %>% filter(species == "queru", canopy == "open", site == "cfc")) %>% summary()
## formula: stage ~ doy + heat + water + heat_water + heat_doy + water_doy
## data: df
##
## link threshold nobs logLik AIC niter max.grad cond.H
## logit flexible 1193 -814.79 1645.58 6(0) 8.76e-11 9.5e+07
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## doy 0.16736 0.01033 16.205 < 2e-16 ***
## heat 3.63363 0.98145 3.702 0.000214 ***
## water 1.31675 1.73531 0.759 0.447972
## heat_water -0.11394 0.17484 -0.652 0.514627
## heat_doy -0.01961 0.00627 -3.127 0.001764 **
## water_doy -0.01152 0.01062 -1.085 0.278045
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Threshold coefficients:
## Estimate Std. Error z value
## budbreak|oneleaf 25.233 1.620 15.57
## oneleaf|mostleaf 27.858 1.668 16.70
Results of ordinal regression interpreted as follows
- Stage progresses over time in a spring
- Warming leads to earlier development
- Stronger warming leads to even earlier development
- Rainfall reduction leads to earlier development
- Interaction between warming and drying offsets advancement (not conclusive)
- Warming slows down the pace of development (not conclusive)
- Rainfall reduction slows down the pace of development (not conclusive)
Future directions
Questions
- Model convergence issue?
- What to do when categories are overlapping?
Short-term improvements
- Fixed effects for site, canopy, species, background climate
- Random effects for block
- Choice of link function (currently logit)
- Add “dormancy” category
Long-term developments
- Changing the function for latent variable (currently linear)